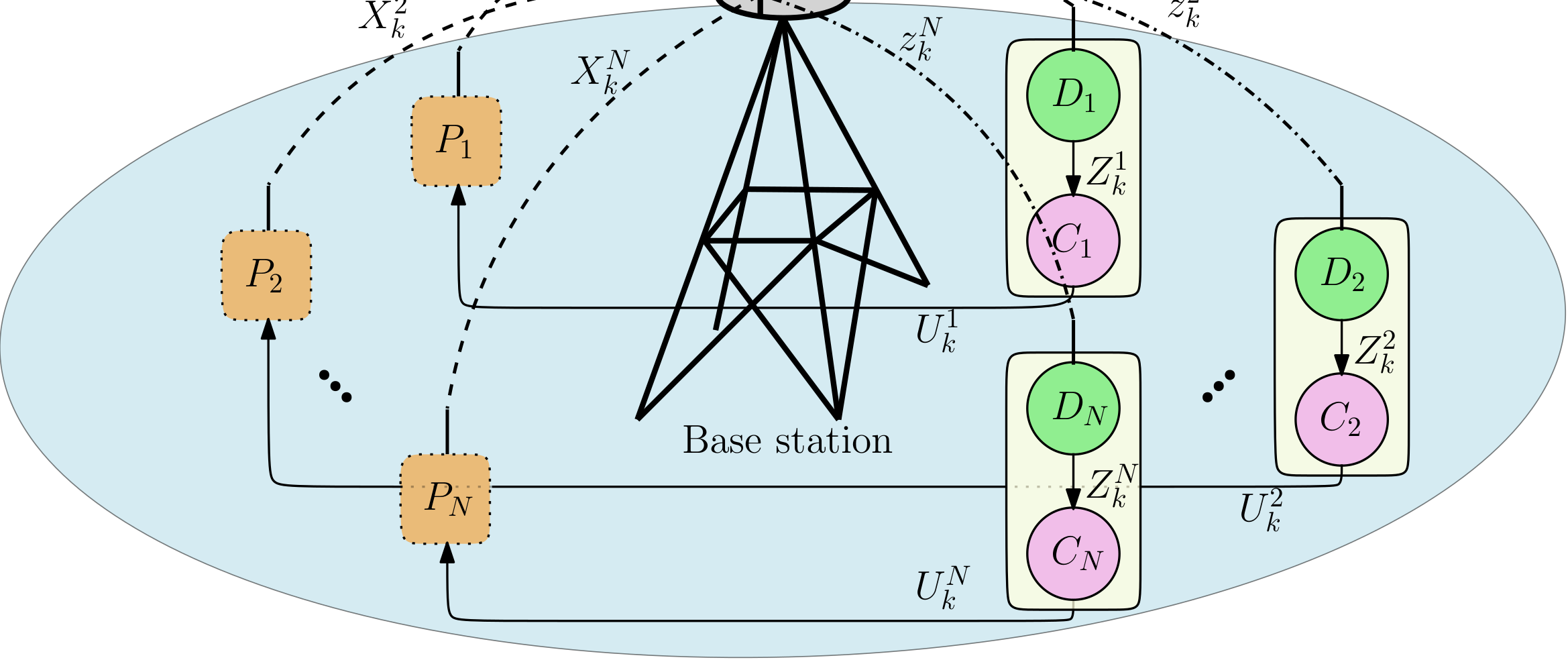
This paper studies an $N$--agent cost-coupled game where the agents are connected via an unreliable capacity constrained network. Each agent receives state information over that network which loses packets with probability $p$. A Base station (BS) actively schedules agent communications over the network by minimizing a weighted Age of Information (WAoI) based cost function under a capacity limit $\mathcal{C} < N$ on the number of transmission attempts at each instant. Under a standard information structure, we show that the problem can be decoupled into a scheduling problem for the BS and a game problem for the $N$ agents. Since the scheduling problem is an NP hard combinatorics problem, we propose an approximately optimal solution which approaches the optimal solution as $N \rightarrow \infty$. In the process, we also provide some insights on the case without channel erasure. Next, to solve the large population game problem, we use the mean-field game framework to compute an approximate decentralized Nash equilibrium. Finally, we validate the theoretical results using a numerical example.
翻译:----
本文研究了一个由N个代理组成的费用耦合博弈,这些代理通过不可靠的容量约束网络相连。每个代理通过这个网络接收状态信息,但这个网络会以概率p丢失数据包。一个基站(BS)按照一定的容量限制($\mathcal{C} < N$)以及最小化基于信息时代的加权成本函数的原则主动调度代理的通信。在标准信息结构下,我们表明该问题可以被分解为BS的调度问题和N个代理的博弈问题。由于调度问题是一个NP难的组合问题,我们提出了一种近似最优解,当$N \rightarrow \infty$时,这个解接近最优解。我们也为没有信道抹除的情况提供了一些见解。接下来,为了解决大规模人口博弈问题,我们使用均值场游戏框架计算近似分散纳什均衡。最后,我们使用数值实例验证了理论结果。