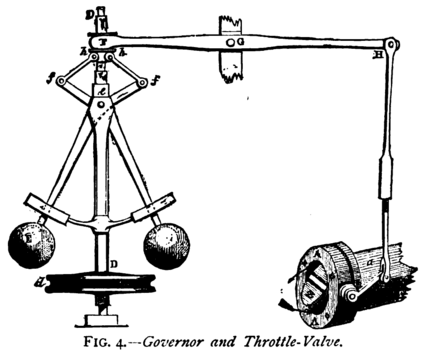
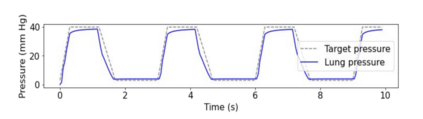
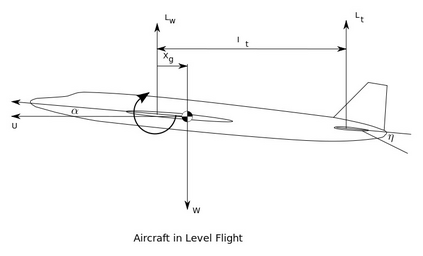
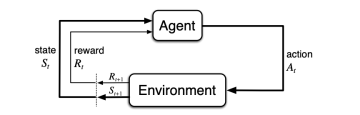
This text presents an introduction to an emerging paradigm in control of dynamical systems and differentiable reinforcement learning called online nonstochastic control. The new approach applies techniques from online convex optimization and convex relaxations to obtain new methods with provable guarantees for classical settings in optimal and robust control. The primary distinction between online nonstochastic control and other frameworks is the objective. In optimal control, robust control, and other control methodologies that assume stochastic noise, the goal is to perform comparably to an offline optimal strategy. In online nonstochastic control, both the cost functions as well as the perturbations from the assumed dynamical model are chosen by an adversary. Thus the optimal policy is not defined a priori. Rather, the target is to attain low regret against the best policy in hindsight from a benchmark class of policies. This objective suggests the use of the decision making framework of online convex optimization as an algorithmic methodology. The resulting methods are based on iterative mathematical optimization algorithms, and are accompanied by finite-time regret and computational complexity guarantees.
翻译:本文本介绍了一种新兴模式,即控制动态系统和不同强化学习的新兴范例,称为在线非随机控制。新办法采用在线调试优化和调试放松技术,以优化和稳健控制的方式获得对古典环境具有可验证保障的新方法。对在线非随机控制和其他框架的主要区分是目标。在优化控制、稳健控制和其他假定随机噪音的控制方法中,目标是与离线最佳战略相对应。在在线非随机控制中,成本功能以及假设动态模型的干扰均由对手选择。因此,最佳政策没有先验定义。相反,目标是在从基准政策类别中后视的最佳政策面前实现低遗憾。这个目标是用决定框架将在线调控控优化作为一种算法。由此产生的方法以迭代数学优化算法为基础,并伴有限定时间的遗憾和计算复杂性保证。