Rate-Exponent Region for a Class of Distributed Hypothesis Testing Against Conditional Independence Problems

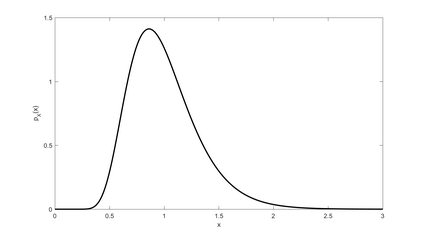
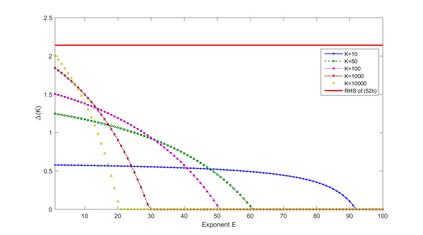
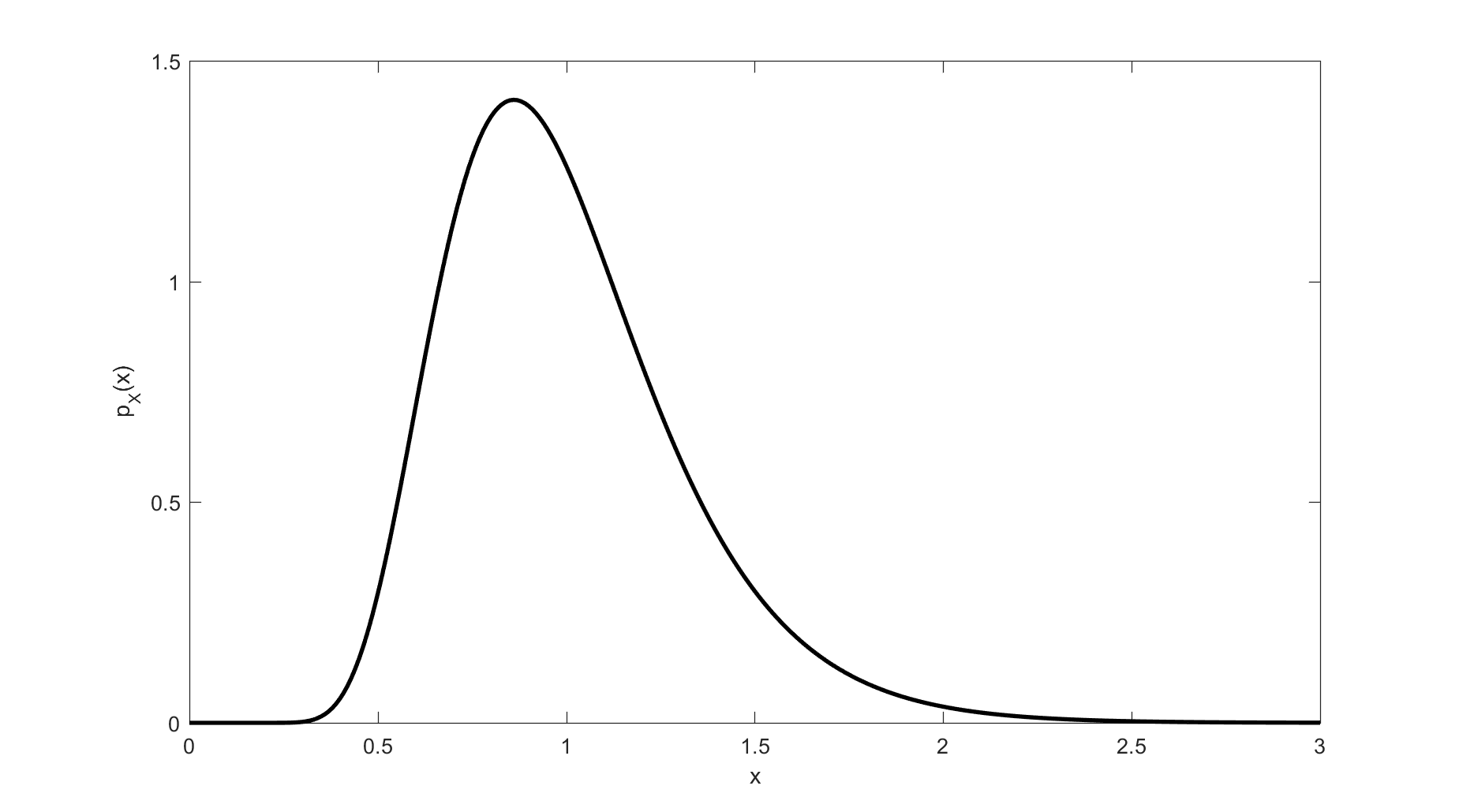
We study a class of $K$-encoder hypothesis testing against conditional independence problems. Under the criterion that stipulates minimization of the Type II error exponent subject to a (constant) upper bound $\epsilon$ on the Type I error rate, we characterize the set of encoding rates and exponent for both discrete memoryless and memoryless vector Gaussian settings. For the DM setting, we provide a converse proof and show that it is achieved using the Quantize-Bin-Test scheme of Rahman and Wagner. For the memoryless vector Gaussian setting, we develop a tight outer bound by means of a technique that relies on the de Bruijn identity and the properties of Fisher information. In particular, the result shows that for memoryless vector Gaussian sources the rate-exponent region is exhausted using the Quantize-Bin-Test scheme with Gaussian test channels; and there is no loss in performance caused by restricting the sensors' encoders not to employ time sharing. Furthermore, we also study a variant of the problem in which the source, not necessarily Gaussian, has finite differential entropy and the sensors' observations noises under the null hypothesis are Gaussian. For this model, our main result is an upper bound on the exponent-rate function. The bound is shown to mirror a corresponding explicit lower bound, except that the lower bound involves the source power (variance) whereas the upper bound has the source entropy power. Part of the utility of the established bound is for investigating asymptotic exponent/rates and losses incurred by distributed detection as function of the number of sensors.