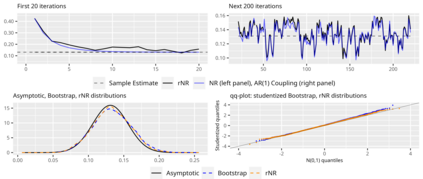
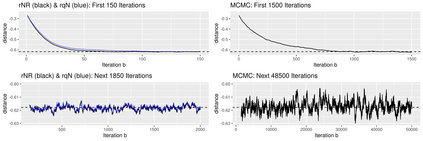
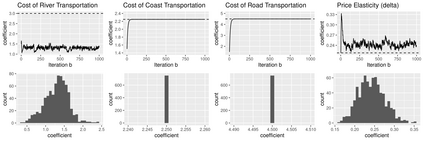
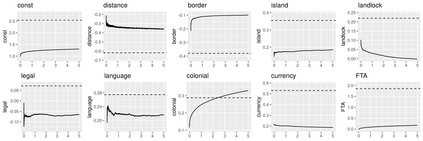
In non-linear estimations, it is common to assess sampling uncertainty by bootstrap inference. For complex models, this can be computationally intensive. This paper combines optimization with resampling: turning stochastic optimization into a fast resampling device. Two methods are introduced: a resampled Newton-Raphson (rNR) and a resampled quasi-Newton (rqN) algorithm. Both produce draws that can be used to compute consistent estimates, confidence intervals, and standard errors in a single run. The draws are generated by a gradient and Hessian (or an approximation) computed from batches of data that are resampled at each iteration. The proposed methods transition quickly from optimization to resampling when the objective is smooth and strictly convex. Simulated and empirical applications illustrate the properties of the methods on large scale and computationally intensive problems. Comparisons with frequentist and Bayesian methods highlight the features of the algorithms.
翻译:在非线性估算中, 通常会通过靴子陷阱推断来评估抽样不确定性。 对于复杂的模型, 它可以进行大量计算。 本文将优化与重新取样相结合: 将随机优化转化为快速再采样设备。 引入了两种方法: 重新标注牛顿- 拉夫森( rNR) 和重新标定准牛顿( rqN) 算法。 两种方法都产生可以用来计算一致的估算、 信任间隔和标准差错的图画。 抽取由梯度和海珊( 或近似) 生成, 由在每次迭代中重新采样的批数据计算出来。 在目标平滑和严格交织时, 拟议的方法会迅速从优化过渡到再采样。 模拟和实验应用可以说明大尺度方法的属性和计算密集问题。 与常客和巴伊斯方法的比较会突出算法的特征 。