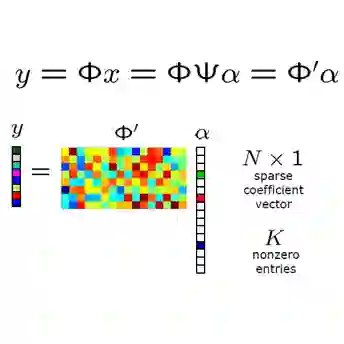
In compressed sensing, the measurement is usually contaminated by additive noise, and hence the information on the noise variance is often required to design algorithms. In this paper, we propose an estimation method for the unknown noise variance in compressed sensing problems. The proposed method, called asymptotic residual matching (ARM), estimates the noise variance from a single measurement vector on the basis of the asymptotic result for the $\ell_{1}$ optimization problem. Specifically, we derive the asymptotic residual corresponding to the $\ell_{1}$ optimization and show that it depends on the noise variance. The proposed ARM approach obtains the estimate by comparing the asymptotic residual with the actual one, which can be obtained by the empirical reconstruction without the information of the noise variance. For the proposed ARM, we also propose a method to choose a reasonable parameter on the basis of the asymptotic residual as well. The idea of the proposed ARM can be applied not only to the reconstruction of the sparse vector but also to that of other structured vectors such as the binary vector. Simulation results show that the proposed noise variance estimation outperforms several conventional methods, especially when the problem size is small. We also show that, by using the proposed method, we can tune the regularization parameter of the $\ell_{1}$ optimization to achieve good reconstruction performance even when the noise variance is unknown.
翻译:在压缩遥感中,测量通常受到添加噪音的污染,因此,设计算法往往需要关于噪声差异的信息。在本文中,我们建议了对压缩遥感问题中未知噪音差异的估算方法。拟议方法称为无症状残留比对(ARM),根据对$@ ⁇ 1美元优化问题的无症状结果,估计单一测量矢量的噪音差异。具体地说,我们得出与耗氧病媒重建相对应的无症状残留量,并表明它取决于噪声差异。拟议的ARM方法通过将无症状残留量与实际残留量进行比较而获得这一估算。在没有噪音差异信息的情况下,可以通过经验重建获得这一估算。对于拟议的ARM,我们还提出了一个方法,根据无症状残余量的无症状影响估计结果来选择一个合理的参数。 拟议的ARM不仅可以适用于稀释病媒的重建,还可以适用于其他结构化病媒,例如二进量矢量。 模拟结果显示,拟议的噪声差异估计值比值是若干常规方法,当我们用不确定的方法来调整时,我们也可以用不确定的比值调整。