A Stable Implementation of a Well-posed 2-D Curvilinear Shallow Water Equations with No-Penetration Wall and Far-Field Boundary conditions

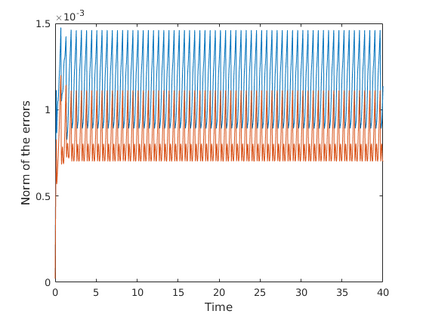
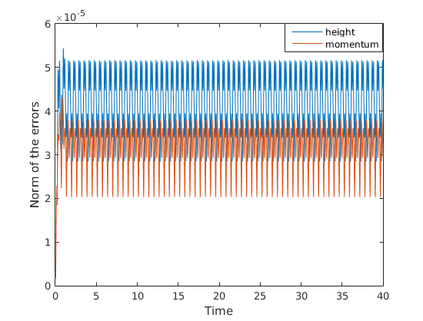
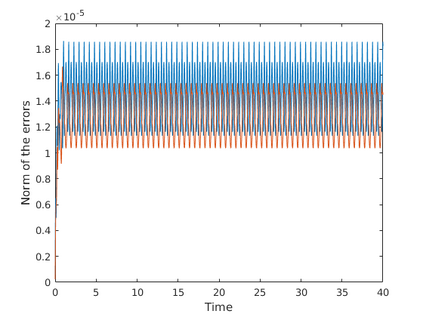
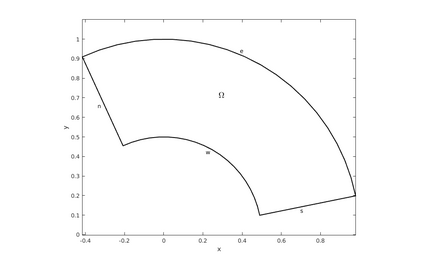
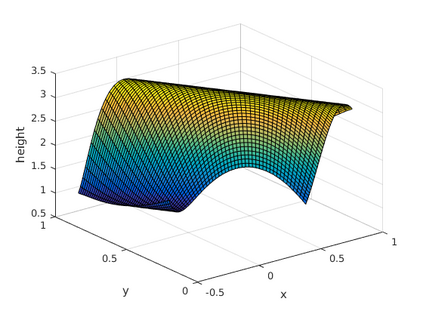
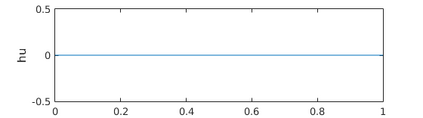
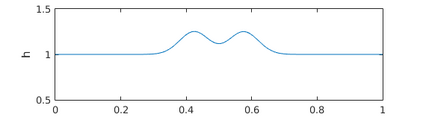
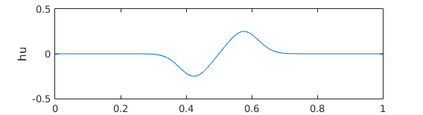
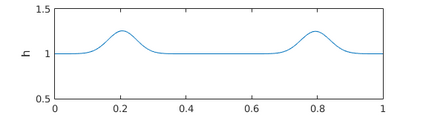
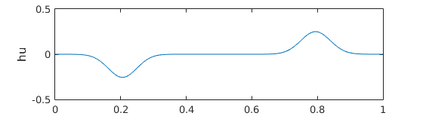
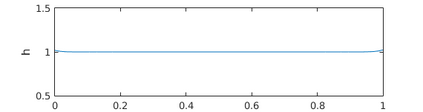
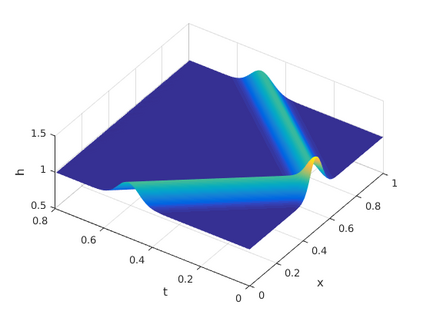
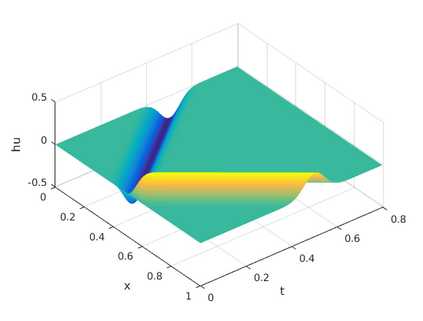
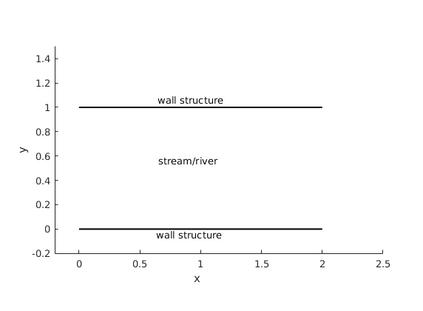
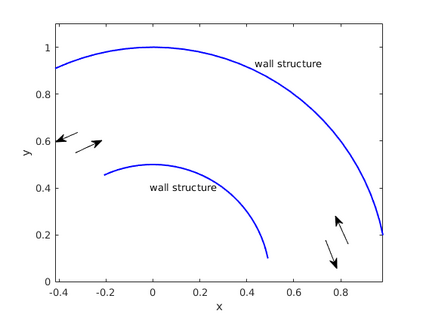
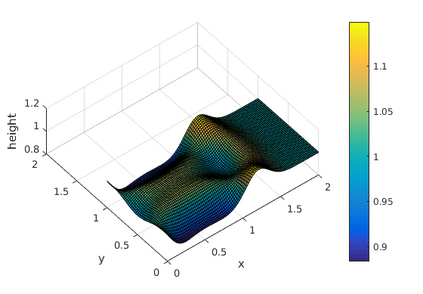
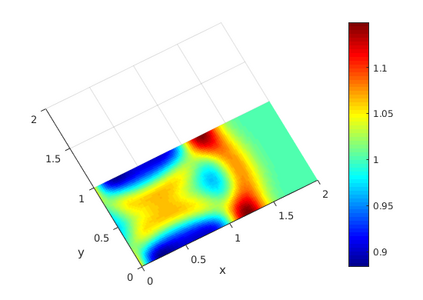
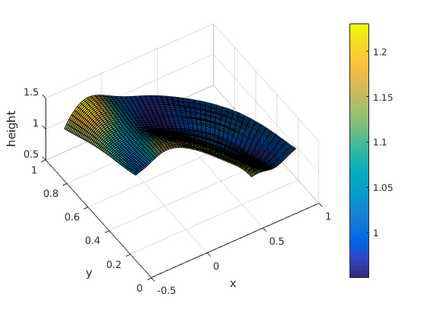
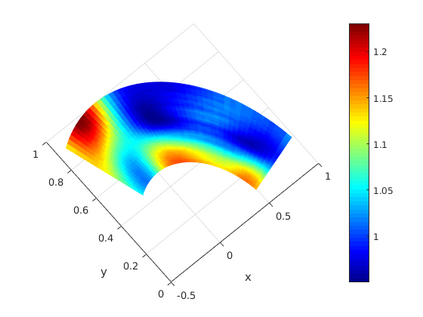
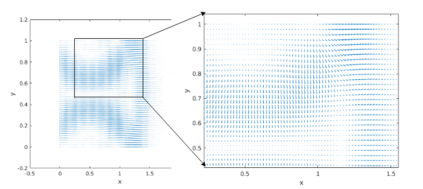
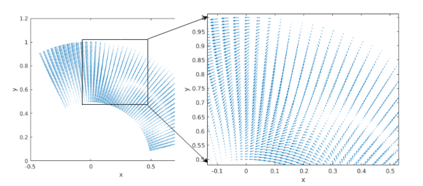
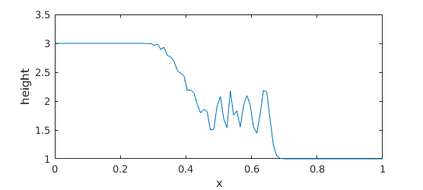
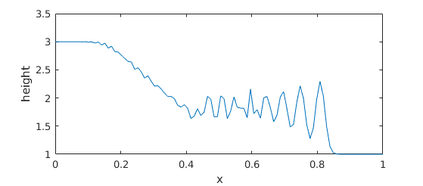
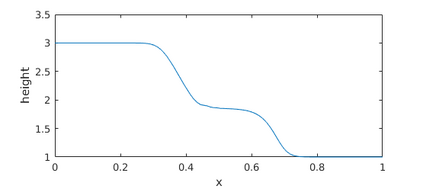
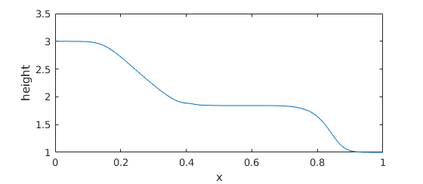
This paper presents a more stable implementation and a highly accurate numerical tool for predicting flooding in urban areas. We started with the (linearised) well-posedness analysis by [1], where far-field boundary conditions were proposed but extended their analysis to include wall boundaries. Specifically, high-order Summation-by-parts (SBP) finite-difference operators were employed to construct a scheme for the Shallow Water Equations. Subsequently, a stable SBP scheme with Simultaneous Approximation Terms that imposes both far-field and wall boundaries was developed. Finally, we extended the schemes and their stability proofs to non-cartesian domains. To demonstrate the strength of the schemes, computations for problems with exact solutions were performed and a theoretical design-order with second-, third- and fourth (2,3,4) convergence rates obtained. Finally, we apply the 4th-order scheme to steady river channel, canal (or flood control channel simulations), and dam-break problems. The results show that the imposition of the boundary conditions are stable, and that they cause no visible reflections at the boundaries. The analysis adequately becomes necessary in flood risk management decisions since they can confirm stable and accurate future predictions of floodplain variables