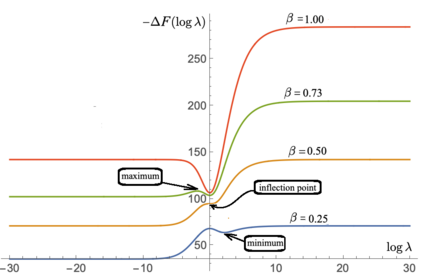
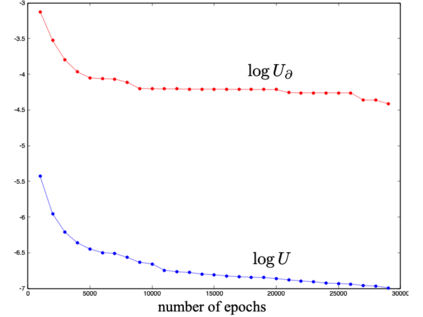
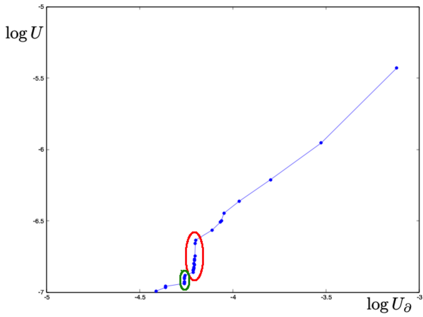
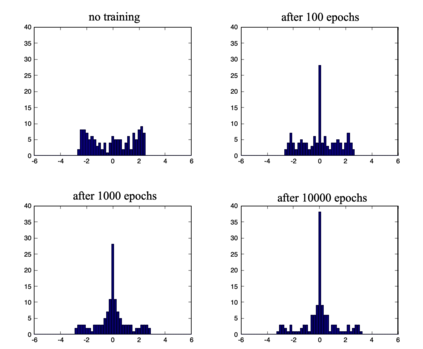
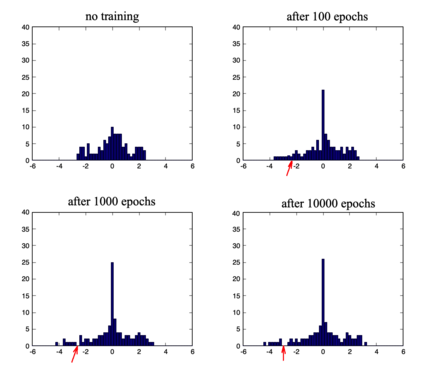
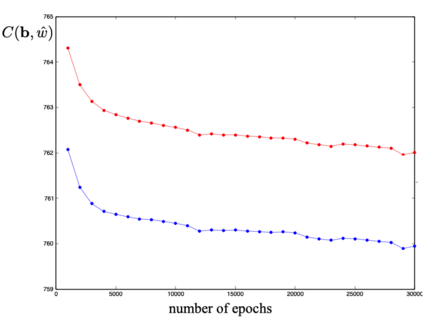
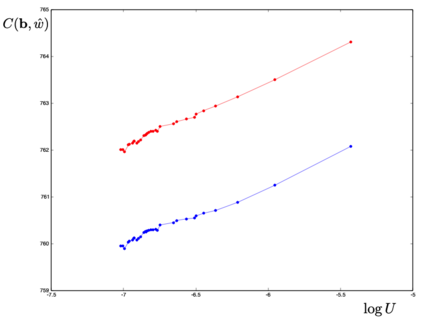
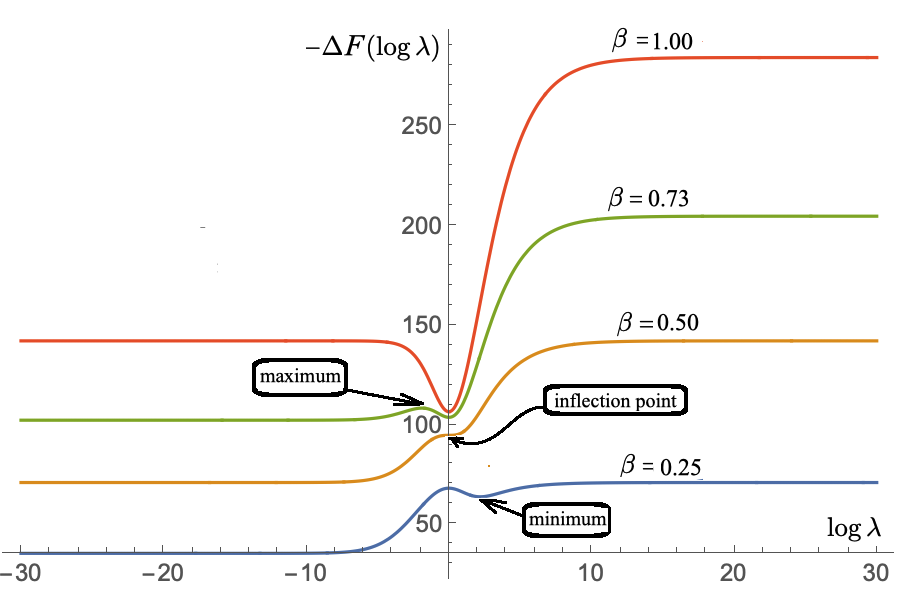
We define a neural network as a septuple consisting of (1) a state vector, (2) an input projection, (3) an output projection, (4) a weight matrix, (5) a bias vector, (6) an activation map and (7) a loss function. We argue that the loss function can be imposed either on the boundary (i.e. input and/or output neurons) or in the bulk (i.e. hidden neurons) for both supervised and unsupervised systems. We apply the principle of maximum entropy to derive a canonical ensemble of the state vectors subject to a constraint imposed on the bulk loss function by a Lagrange multiplier (or an inverse temperature parameter). We show that in an equilibrium the canonical partition function must be a product of two factors: a function of the temperature and a function of the bias vector and weight matrix. Consequently, the total Shannon entropy consists of two terms which represent respectively a thermodynamic entropy and a complexity of the neural network. We derive the first and second laws of learning: during learning the total entropy must decrease until the system reaches an equilibrium (i.e. the second law), and the increment in the loss function must be proportional to the increment in the thermodynamic entropy plus the increment in the complexity (i.e. the first law). We calculate the entropy destruction to show that the efficiency of learning is given by the Laplacian of the total free energy which is to be maximized in an optimal neural architecture, and explain why the optimization condition is better satisfied in a deep network with a large number of hidden layers. The key properties of the model are verified numerically by training a supervised feedforward neural network using the method of stochastic gradient descent. We also discuss a possibility that the entire universe on its most fundamental level is a neural network.
翻译:我们定义了神经网络, 包括:(1) 状态矢量, (2) 输入投影, (3) 输出投影, (4) 重量矩阵, (5) 偏向矢量, (6) 激活映射, (7) 损失函数。 我们争论说, 损失函数既可以在边界( 输入和/ 输出神经元) 上, 也可以在大宗( 隐藏神经元) 中( 隐藏神经元) 强加。 我们应用最大星盘原则, 以获得恒温动力的导体和神经网络的复杂性来获取状态矢量的共合体。 我们运用了最大星盘原则, 受Lagrange 倍增增量函数( 或低温矩阵) 约束, (5) 重增量矩阵值 。 在平衡中, 罐体分割函数必须是两个因素的产物 : 温度函数和偏移值的函数。 因此, 香农总恒温变量和神经网络的模型的复杂性能。 我们得出了第一个和第二个测算法 : 在学习整个恒变量中, 整个系统必须降低, 直至系统进入一个精度的精度值, 直至最深的系统进入一个精度变压的精度变数 。 。