Quantum and Probabilistic Computers Rigorously Powerful than Traditional Computers, and Derandomization

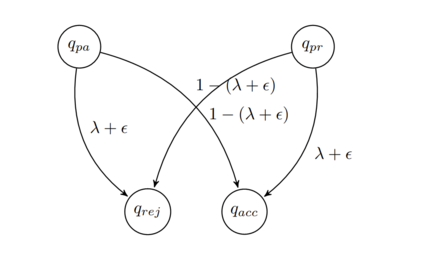
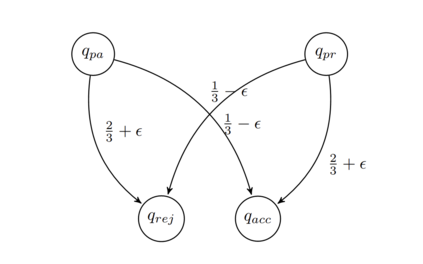
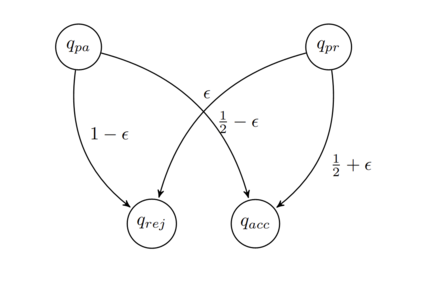
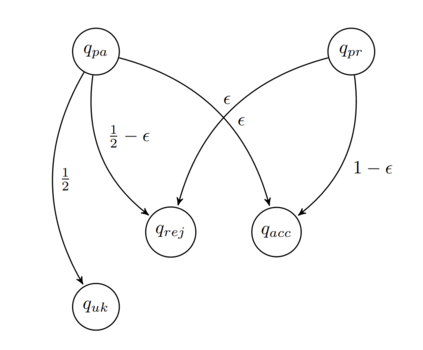
In this paper, we extend the techniques used in our previous work to show that there exists a probabilistic Turing machine running within time $O(n^k)$ for all $k\in\mathbb{N}_1$ accepting a language $L_d$ which is different from any language in $\mathcal{P}$, and then to show that $L_d\in\mathcal{BPP}$, thus separating the complexity classes $\mathcal{P}$ and $\mathcal{BPP}$ (i.e., $\mathcal{P}\subsetneq\mathcal{BPP}$). Since the complexity class of {\em bounded error quantum polynomial-time} $\mathcal{BQP}$ contains the complexity class $\mathcal{BPP}$, i.e., $\mathcal{BPP}\subseteq\mathcal{BQP}$, we thus obtain the result that quantum computers are {\em rigorously powerful than} traditional computers. Namely, $\mathcal{P}\subsetneq\mathcal{BQP}$. We further show that (1). $\mathcal{P}\subsetneq\mathcal{RP}$; (2). $\mathcal{P}\subsetneq\text{co-}\mathcal{RP}$; (3). $\mathcal{P}\subsetneq\mathcal{ZPP}$. The result of $\mathcal{P}\subsetneq\mathcal{BPP}$ shows that {\em randomness} plays an essential role in probabilistic algorithm design. Specifically, we show that: (1). The number of random bits used by any probabilistic algorithm which accepts the language $L_d$ can not be reduced to $O(\log n)$; (2). There exits no efficient (complexity-theoretic) {\em pseudorandom generator} (PRG) $G:\{0,1\}^{O(\log n)}\rightarrow \{0,1\}^n$; (3). There exists no quick HSG $H:k(n)\rightarrow n$ such that $k(n)=O(\log n)$.