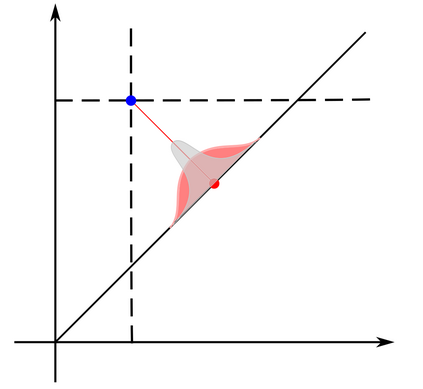
Computing sample means on Riemannian manifolds is typically computationally costly as exemplified by computation of the Fr\'echet mean which often requires finding minimizing geodesics to each data point for each step of an iterative optimization scheme. When closed-form expressions for geodesics are not available, this leads to a nested optimization problem that is costly to solve. The implied computational cost impacts applications in both geometric statistics and in geometric deep learning. The weighted diffusion mean offers an alternative to the weighted Fr\'echet mean. We show how the diffusion mean and the weighted diffusion mean can be estimated with a stochastic simulation scheme that does not require nested optimization. We achieve this by conditioning a Brownian motion in a product manifold to hit the diagonal at a predetermined time. We develop the theoretical foundation for the sampling-based mean estimation, we develop two simulation schemes, and we demonstrate the applicability of the method with examples of sampled means on two manifolds.
翻译:计算器样本意味着里曼尼方块的计算费用通常很高,如Fr\'echet 平均值的计算,通常需要找到一个迭代优化方案每个步骤的每个数据点的最小大地测量值。当没有大地测量仪的封闭式表达式时,这会导致一个嵌套式优化问题,这个问题需要解决,在几何统计和几何深学习中隐含的计算成本影响应用。加权扩散意味着一个加权Fr\'echet 平均值的替代物。我们用一个不需要嵌套优化的随机模拟方案来估计扩散值和加权扩散值。我们通过在产品元体中调节布朗尼运动,以便在预定的时间撞击对角。我们为基于取样的平均值估算开发理论基础,我们开发两个模拟方案,我们用两个公式的抽样方法实例来展示方法的适用性。