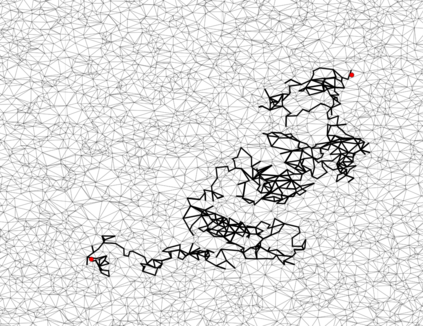
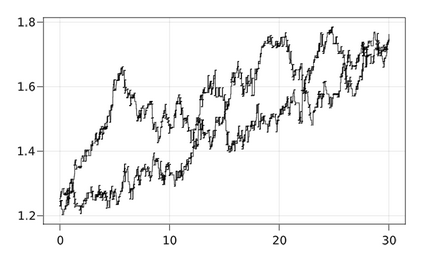
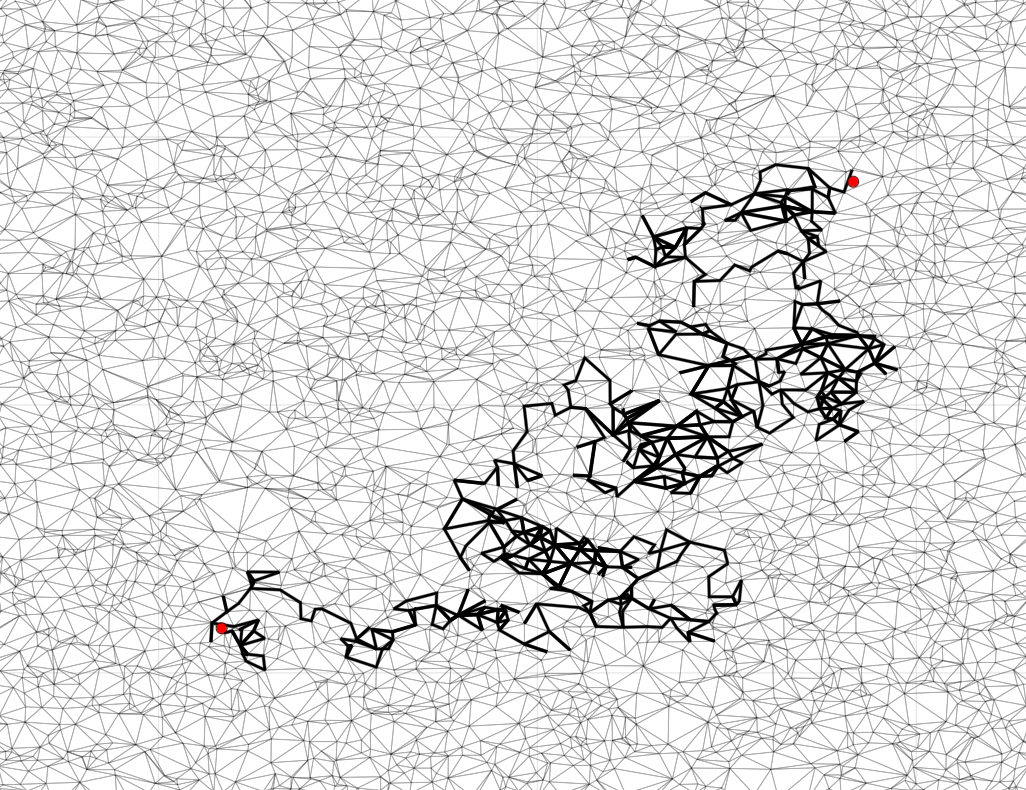
A continuous-time Markov process $X$ can be conditioned to be in a given state at a fixed time $T > 0$ using Doob's $h$-transform. This transform requires the typically intractable transition density of $X$. The effect of the $h$-transform can be described as introducing a guiding force on the process. Replacing this force with an approximation defines the wider class of guided processes. For certain approximations the law of a guided process approximates - and is equivalent to - the actual conditional distribution, with tractable likelihood-ratio. The main contribution of this paper is to prove that the principle of a guided process, introduced in Schauer et al. (2017) for stochastic differential equations, can be extended to a more general class of Markov processes. In particular we apply the guiding technique to jump processes in discrete state spaces. The Markov process perspective enables us to improve upon existing results for hypo-elliptic diffusions.
翻译:连续时间 Markov 工艺 $X$可以有条件地在固定时间 $T > 0美元 的状态下使用 Doob 的 $h$- transform 。 这种转变需要通常难以控制的过渡密度 $X$。 $h$- transform 的效果可以描述为在工艺中引入一种指导力量。 以近似值取代这一力量定义了更宽的引导工艺类别。 对于某些近似点来说, 指导工艺的定律近似 - - - - - - - - - - - - - 相当于实际有条件的分布, 并具有可移动的可能性 - 。 本文的主要贡献是证明 Schauer 等人( 2017年) 引入的制导过程原则可以推广到更一般的 Markov 进程类别 。 我们特别将指导技术应用于离散状态空间的跳跃动过程 。 Markov 进程观点使我们能够改进低电子扩散的现有结果 。