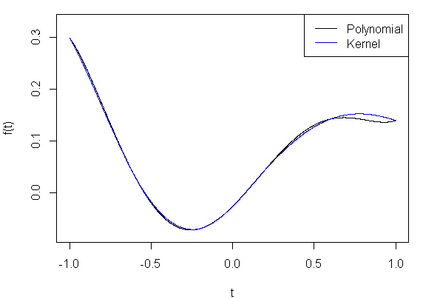
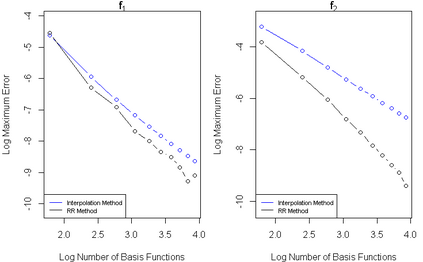
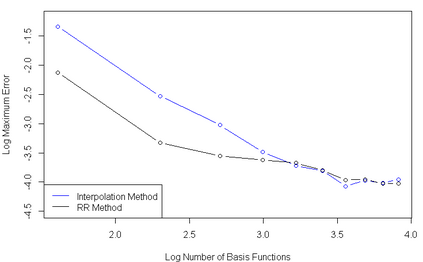
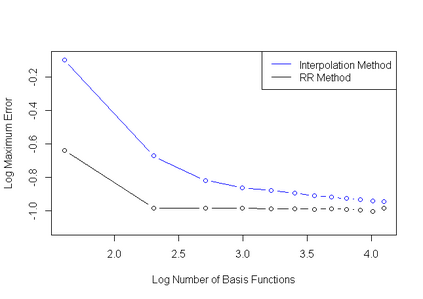
Gaussian processes are among the most useful tools in modeling continuous processes in machine learning and statistics. If the value of a process is known at a finite collection of points, one may use Gaussian processes to construct a surface which interpolates these values to be used for prediction and uncertainty quantification in other locations. However, it is not always the case that the available information is in the form of a finite collection of points. For example, boundary value problems contain information on the boundary of a domain, which is an uncountable collection of points that cannot be incorporated into typical Gaussian process techniques. In this paper we construct a Gaussian process model which utilizes reproducing kernel Hilbert spaces to unify the typical finite case with the case of having uncountable information by exploiting the equivalence of conditional expectation and orthogonal projections. We discuss this construction in statistical models, including numerical considerations and a proof of concept.
翻译:高斯进程是模拟机器学习和统计连续过程的最有用工具之一。如果一个过程的价值在有限的点数收集中已知,人们可以使用高斯进程来构建一个表面,将这些数值用于其他地点的预测和不确定性量化,然而,现有信息并不总是以有限的点数收集的形式出现。例如,边界值问题包含一个域域的边界信息,这是一个无法计算、无法纳入典型高斯进程技术的点数收集。在本文中,我们构建了一个高斯进程模型,利用再生产内核希尔伯特空间来统一典型的有限案例,通过利用有条件期望和孔数预测的等值来统一不可计算的信息。我们用统计模型来讨论这一构建,包括数字考虑和概念证明。