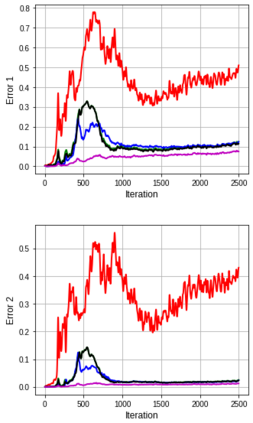
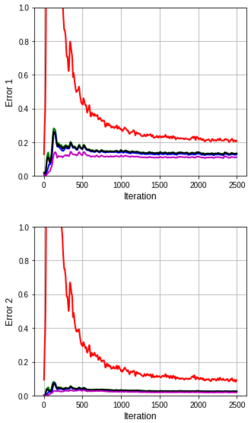
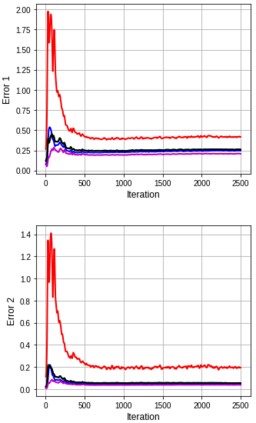
Several studies have shown the ability of natural gradient descent to minimize the objective function more efficiently than ordinary gradient descent based methods. However, the bottleneck of this approach for training deep neural networks lies in the prohibitive cost of solving a large dense linear system corresponding to the Fisher Information Matrix (FIM) at each iteration. This has motivated various approximations of either the exact FIM or the empirical one. The most sophisticated of these is KFAC, which involves a Kronecker-factored block diagonal approximation of the FIM. With only a slight additional cost, a few improvements of KFAC from the standpoint of accuracy are proposed. The common feature of the four novel methods is that they rely on a direct minimization problem, the solution of which can be computed via the Kronecker product singular value decomposition technique. Experimental results on the three standard deep auto-encoder benchmarks showed that they provide more accurate approximations to the FIM. Furthermore, they outperform KFAC and state-of-the-art first-order methods in terms of optimization speed.
翻译:一些研究显示,自然梯度下降能够比普通梯度下降法更高效地最大限度地减少客观功能,但是,这种培训深神经网络的方法的瓶颈在于每次迭代解决与渔业信息矩阵(FIM)相对的大型密集线性系统的费用太高,这促使对准确的FIM或经验性基准进行各种近似,其中最复杂的是KFAC,它涉及FIM的克罗内克尔因素块对角近似。只要略微增加成本,就建议从准确性的角度对KFAC进行一些改进。四种新方法的共同特点是,它们依赖直接的最小化问题,其解决办法可以通过Kronecker产品单值分解法计算。三种标准深度自动电解码基准的实验结果显示,它们为FIM提供了更准确的近似值。此外,它们比KFAC和最先进的第一阶方法最精确的优化速度。