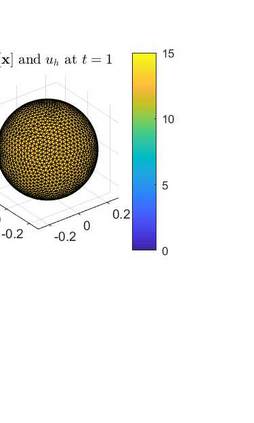
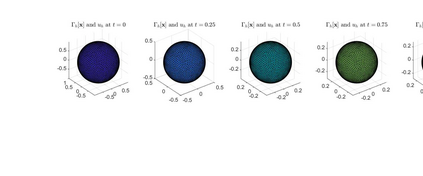
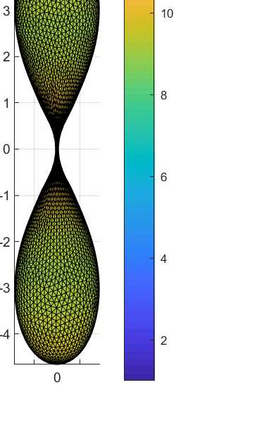
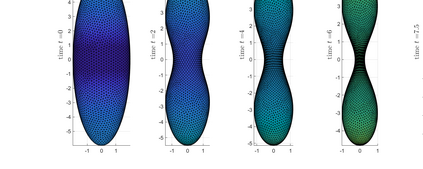
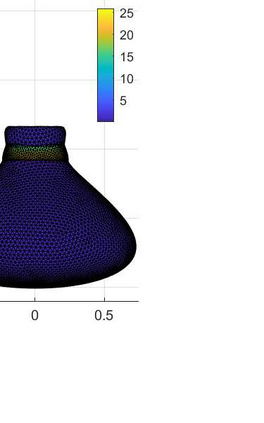
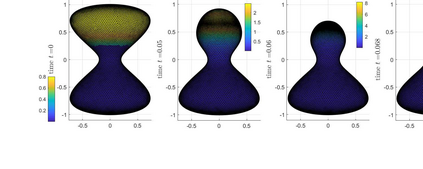
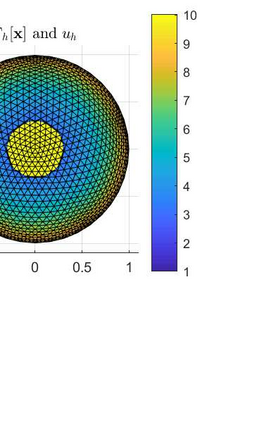
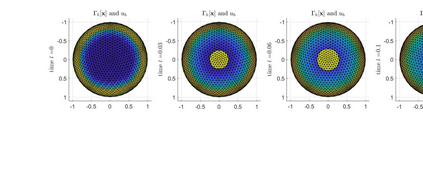
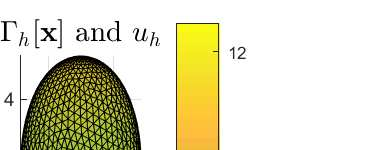An evolving surface finite element discretisation is analysed for the evolution of a closed two-dimensional surface governed by a system coupling a generalised forced mean curvature flow and a reaction--diffusion process on the surface, inspired by a gradient flow of a coupled energy. Two algorithms are proposed, both based on a system coupling the diffusion equation to evolution equations for geometric quantities in the velocity law for the surface. One of the numerical methods is proved to be convergent in the $H^1$ norm with optimal-order for finite elements of degree at least two. We present numerical experiments illustrating the convergence behaviour and demonstrating the qualitative properties of the flow: preservation of mean convexity, loss of convexity, weak maximum principles, and the occurrence of self-intersections.
翻译:对一个封闭的二维表层的演进进行了不断演变的表面限制元素分化分析,该表层受一个系统管理,这个系统将一个一般的强制平均曲线流和一个反应扩散过程结合起来,并受到一个混合能量的梯度流的启发。提出了两种算法,两种算法都基于一个系统,将扩散方程与地表速度法中几何数量的进化方程结合起来。其中一种数字方法被证明在$H1美元规范中趋同,对至少两个程度的有限元素进行最佳排序。我们提出数字实验,说明汇合行为,并展示流动的质量特性:保持平均值的汇合性、凝结性损失、最弱的原理以及自我切分的出现。