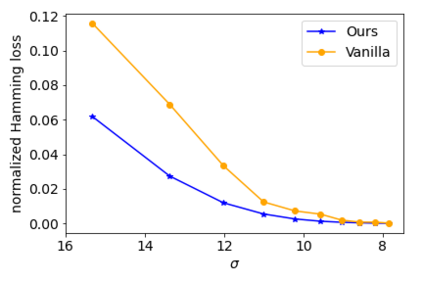
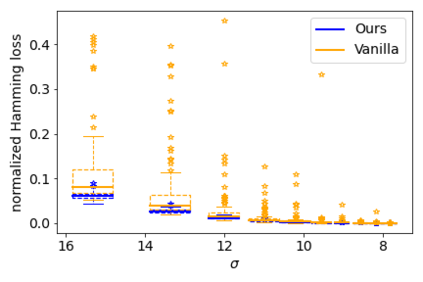
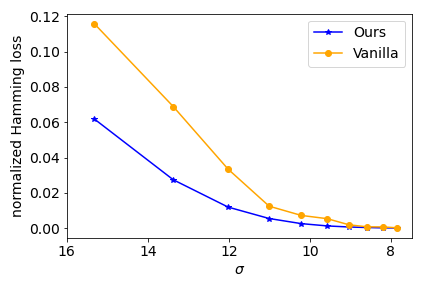
Permutation synchronization is an important problem in computer science that constitutes the key step of many computer vision tasks. The goal is to recover $n$ latent permutations from their noisy and incomplete pairwise measurements. In recent years, spectral methods have gained increasing popularity thanks to their simplicity and computational efficiency. Spectral methods utilize the leading eigenspace $U$ of the data matrix and its block submatrices $U_1,U_2,\ldots, U_n$ to recover the permutations. In this paper, we propose a novel and statistically optimal spectral algorithm. Unlike the existing methods which use $\{U_jU_1^\top\}_{j\geq 2}$, ours constructs an anchor matrix $M$ by aggregating useful information from all the block submatrices and estimates the latent permutations through $\{U_jM^\top\}_{j\geq 1}$. This modification overcomes a crucial limitation of the existing methods caused by the repetitive use of $U_1$ and leads to an improved numerical performance. To establish the optimality of the proposed method, we carry out a fine-grained spectral analysis and obtain a sharp exponential error bound that matches the minimax rate.
翻译:置换同步是计算机科学中的一个重要问题,它构成了许多计算机视觉任务的关键步骤。目标是从含噪声和不完整的成对测量中恢复$n$个潜在的置换。近年来,谱方法因其简单性和计算效率而越来越受到欢迎。谱方法利用数据矩阵及其块子矩阵$U_1,U_2,\ldots,U_n$的主特征空间$U$来恢复置换。在本文中,我们提出了一种新颖且统计上最优的谱算法。与现有方法使用$\{U_jU_1^\top\}_{j\geq 2}$不同,我们通过聚合所有块子矩阵中有用的信息构造一个锚矩阵$M$,并通过$\{U_jM^\top\}_{j\geq 1}$来估计潜在的置换。这种修改克服了现有方法由于重复使用$U_1$而引起的关键限制,并带来了改进的数值性能。为了建立所提出方法的最优性,我们进行了精细的谱分析,并获得了与最小极小化速率相匹配的尖锐指数误差界。