Deinsum: Practically I/O Optimal Multilinear Algebra

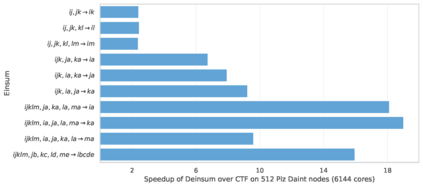
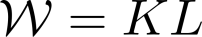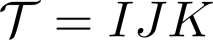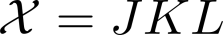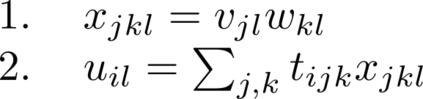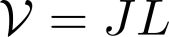Multilinear algebra kernel performance on modern massively-parallel systems is determined mainly by data movement. However, deriving data movement-optimal distributed schedules for programs with many high-dimensional inputs is a notoriously hard problem. State-of-the-art libraries rely on heuristics and often fall back to suboptimal tensor folding and BLAS calls. We present Deinsum, an automated framework for distributed multilinear algebra computations expressed in Einstein notation, based on rigorous mathematical tools to address this problem. Our framework automatically derives data movement-optimal tiling and generates corresponding distributed schedules, further optimizing the performance of local computations by increasing their arithmetic intensity. To show the benefits of our approach, we test it on two important tensor kernel classes: Matricized Tensor Times Khatri-Rao Products and Tensor Times Matrix chains. We show performance results and scaling on the Piz Daint supercomputer, with up to 19x speedup over state-of-the-art solutions on 512 nodes.