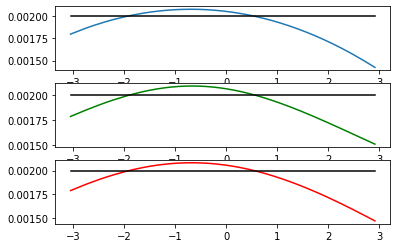
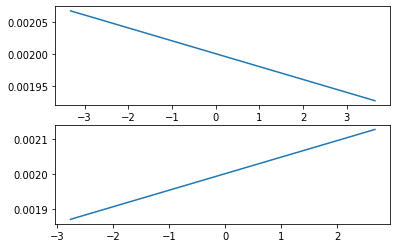
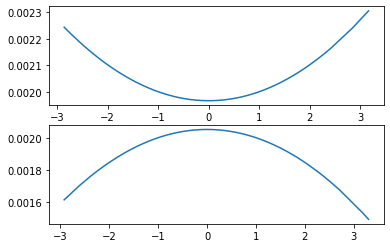
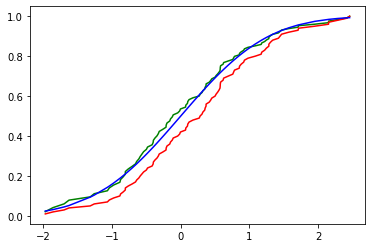
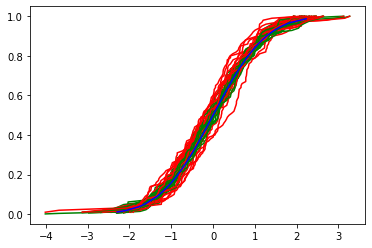
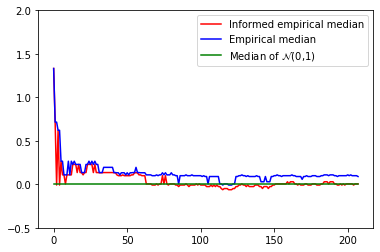
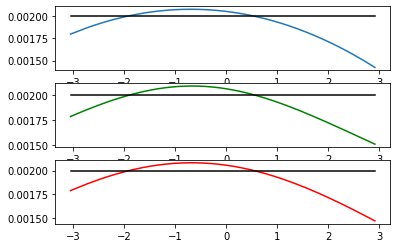
We incorporate into the empirical measure the auxiliary information given by a finite collection of expectation in an optimal information geometry way. This allows to unify several methods exploiting a side information and to uniquely define an informed empirical measure. These methods are shown to share the same asymptotic properties. Then we study the informed empirical process subject to a true information. We establish the Glivenko-Cantelli and Donsker theorems for the informed empirical measure under minimal assumptions and we quantify the asymptotic uniform variance reduction. Moreover, we prove that the informed empirical process is more concentrated than the classical empirical process for all large $n$. Finally, as an illustration of the variance reduction, we apply some of these results to the informed empirical quantiles.
翻译:我们以最佳的信息几何方法将有限收集期望提供的辅助信息纳入实证计量中,这样可以统一几种利用侧边信息的方法,并独到地界定知情的经验计量方法。这些方法被证明具有相同的非现用属性。然后,我们根据真实信息研究知情经验过程。我们根据最低假设为知情经验计量建立Glivenko-Cantelli和Donsker理论,并量化无现用统一差异减少。此外,我们证明知情经验过程比传统经验过程更加集中,所有大额美元。最后,作为差异减少的一个例证,我们将这些结果中的部分应用到知情经验大小中。