Stochastic Prize-Collecting Games: Strategic Planning in Multi-Robot Systems

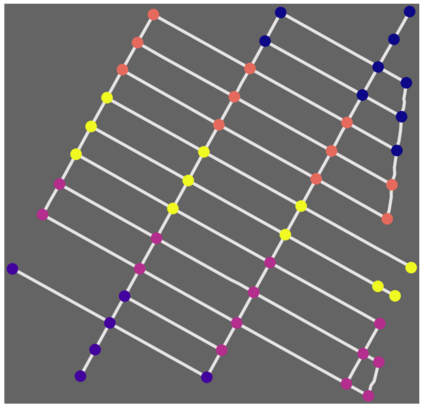
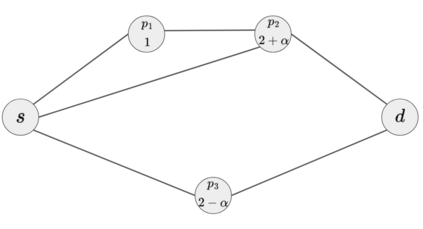
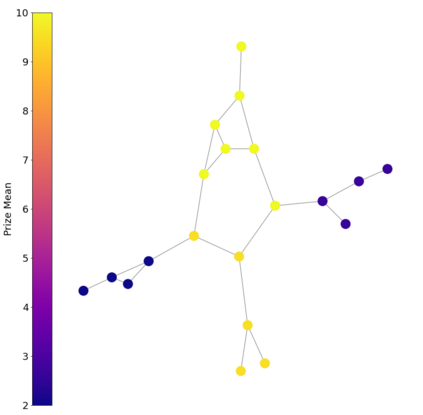
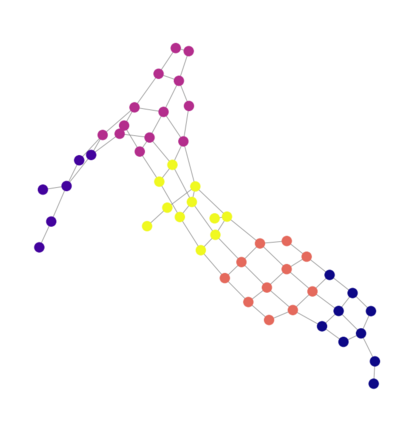
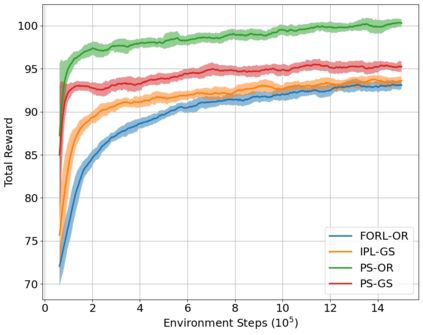
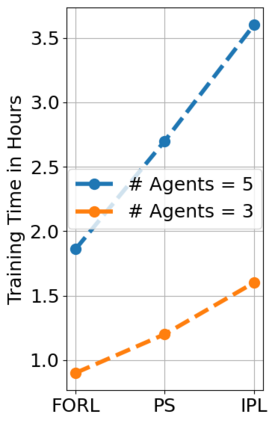
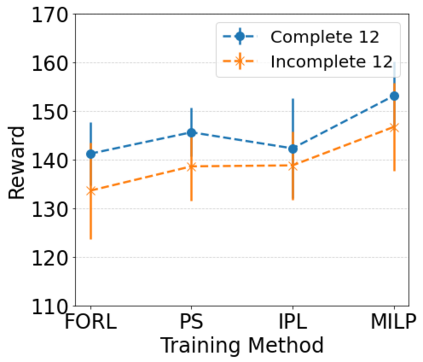
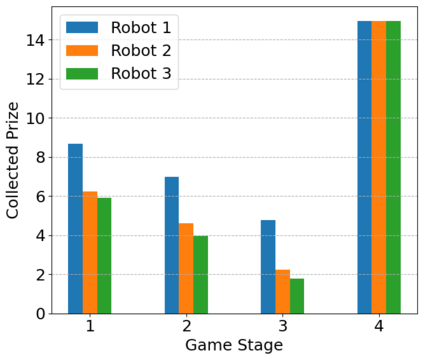
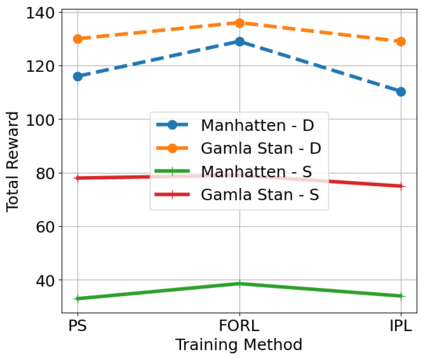
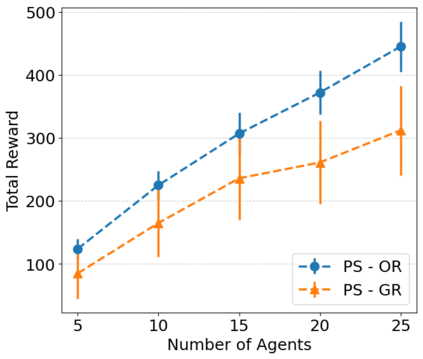
The Team Orienteering Problem (TOP) generalizes many real-world multi-robot scheduling and routing tasks that occur in autonomous mobility, aerial logistics, and surveillance applications. While many flavors of the TOP exist for planning in multi-robot systems, they assume that all the robots cooperate toward a single objective; thus, they do not extend to settings where the robots compete in reward-scarce environments. We propose Stochastic Prize-Collecting Games (SPCG) as an extension of the TOP to plan in the presence of self-interested robots operating on a graph, under energy constraints and stochastic transitions. A theoretical study on complete and star graphs establishes that there is a unique pure Nash equilibrium in SPCGs that coincides with the optimal routing solution of an equivalent TOP given a rank-based conflict resolution rule. This work proposes two algorithms: Ordinal Rank Search (ORS) to obtain the ''ordinal rank'' --one's effective rank in temporarily-formed local neighborhoods during the games' stages, and Fictitious Ordinal Response Learning (FORL) to obtain best-response policies against one's senior-rank opponents. Empirical evaluations conducted on road networks and synthetic graphs under both dynamic and stationary prize distributions show that 1) the state-aliasing induced by OR-conditioning enables learning policies that scale more efficiently to large team sizes than those trained with the global index, and 2) Policies trained with FORL generalize better to imbalanced prize distributions than those with other multi-agent training methods. Finally, the learned policies in the SPCG achieved between 87% and 95% optimality compared to an equivalent TOP solution obtained by mixed-integer linear programming.