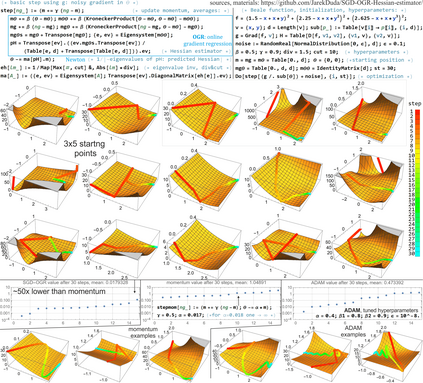
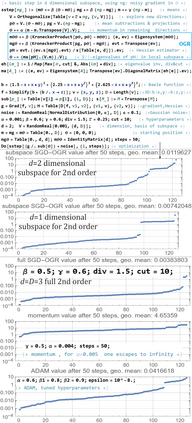
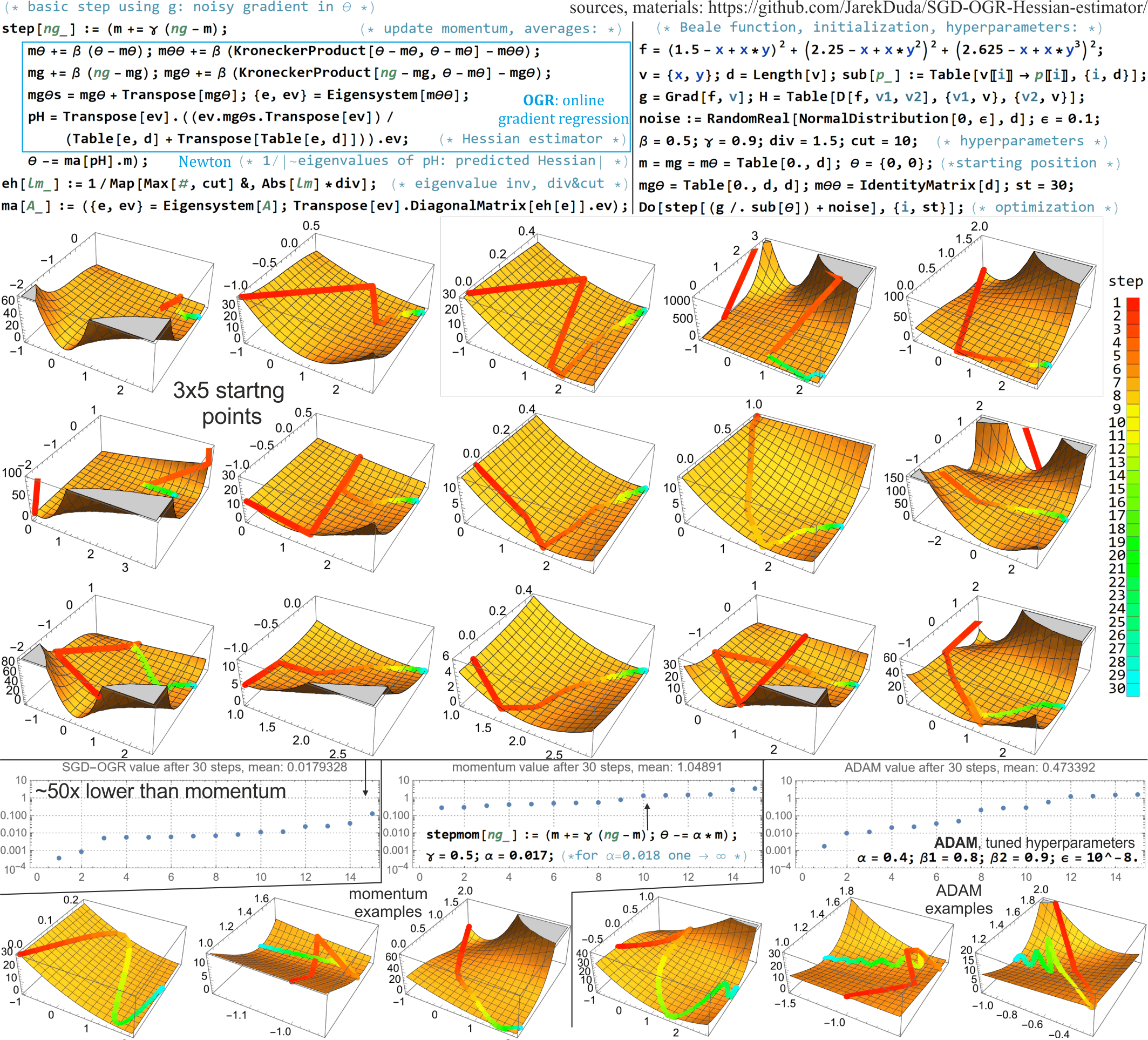
Deep neural networks are usually trained with stochastic gradient descent (SGD), which minimizes objective function using very rough approximations of gradient, only averaging to the real gradient. Standard approaches like momentum or ADAM only consider a single direction, and do not try to model distance from extremum - neglecting valuable information from calculated sequence of gradients, often stagnating in some suboptimal plateau. Second order methods could exploit these missed opportunities, however, beside suffering from very large cost and numerical instabilities, many of them attract to suboptimal points like saddles due to negligence of signs of curvatures (as eigenvalues of Hessian). Saddle-free Newton method is a rare example of addressing this issue - changes saddle attraction into repulsion, and was shown to provide essential improvement for final value this way. However, it neglects noise while modelling second order behavior, focuses on Krylov subspace for numerical reasons, and requires costly eigendecomposion. Maintaining SFN advantages, there are proposed inexpensive ways for exploiting these opportunities. Second order behavior is linear dependence of first derivative - we can optimally estimate it from sequence of noisy gradients with least square linear regression, in online setting here: with weakening weights of old gradients. Statistically relevant subspace is suggested by PCA of recent noisy gradients - in online setting it can be made by slowly rotating considered directions toward new gradients, gradually replacing old directions with recent statistically relevant. Eigendecomposition can be also performed online: with regularly performed step of QR method to maintain diagonal Hessian. Outside the second order modeled subspace we can simultaneously perform gradient descent.
翻译:深心神经网络通常被训练为偏差梯度下行(SGD),这种深心神经网络通常使用非常粗略的梯度近似值来尽量减少客观功能,只是平均到真实的梯度。像动力或ADAM这样的标准方法只考虑一个单一方向,而没有尝试模拟与Exremum的距离 — 忽略了计算出梯度序列的宝贵信息, 往往在某些亚优高原中停滞不前。 第二顺序方法可能会利用这些错失的机会, 但是, 除了代价和数字不稳定性非常大之外, 许多这样的方法会吸引到低于最优化的点, 比如由于曲度迹象( 作为Hessian的偏差值方向)的偏差而吸引到真正的梯度。 Sadle- free Newton 方法是解决这一问题的一个罕见的例子 — 改变马鞍吸引到反转, 并显示为最终值提供了必要的改进。 然而, 在模拟第二顺序行为的同时, 侧重于 Krylov 子空间, 并且需要昂贵的 eigendendecom recocoom 。 保持 Serview 的优势, 有利用这些机会的便宜的方法 。 第二顺序行为行为行为表现是用来的 。