The Best Arm Evades: Near-optimal Multi-pass Streaming Lower Bounds for Pure Exploration in Multi-armed Bandits

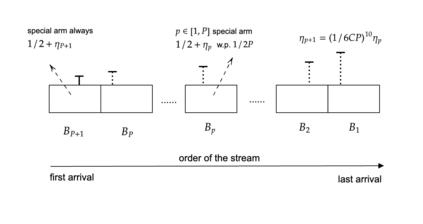
We give a near-optimal sample-pass trade-off for pure exploration in multi-armed bandits (MABs) via multi-pass streaming algorithms: any streaming algorithm with sublinear memory that uses the optimal sample complexity of $O(\frac{n}{\Delta^2})$ requires $\Omega(\frac{\log{(1/\Delta)}}{\log\log{(1/\Delta)}})$ passes. Here, $n$ is the number of arms and $\Delta$ is the reward gap between the best and the second-best arms. Our result matches the $O(\log(\frac{1}{\Delta}))$-pass algorithm of Jin et al. [ICML'21] (up to lower order terms) that only uses $O(1)$ memory and answers an open question posed by Assadi and Wang [STOC'20].