Non-smooth and Hölder-smooth Submodular Maximization

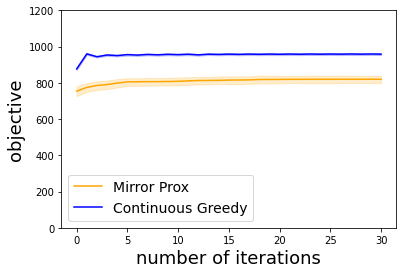
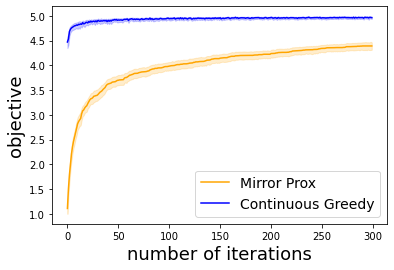
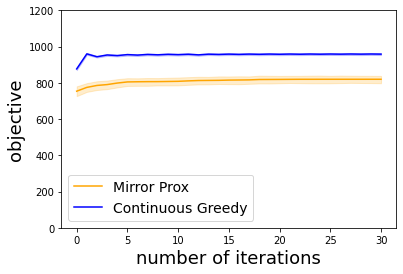
We study the problem of maximizing a continuous DR-submodular function that is not necessarily smooth. We prove that the continuous greedy algorithm achieves an $[(1-1/e)\text{OPT}-\epsilon]$ guarantee when the function is monotone and H\"older-smooth, meaning that it admits a H\"older-continuous gradient. For functions that are non-differentiable or non-smooth, we propose a variant of the mirror-prox algorithm that attains an $[(1/2)\text{OPT}-\epsilon]$ guarantee. We apply our algorithmic frameworks to robust submodular maximization and distributionally robust submodular maximization under Wasserstein ambiguity. In particular, the mirror-prox method applies to robust submodular maximization to obtain a single feasible solution whose value is at least $(1/2)\text{OPT}-\epsilon$. For distributionally robust maximization under Wasserstein ambiguity, we deduce and work over a submodular-convex maximin reformulation whose objective function is H\"older-smooth, for which we may apply both the continuous greedy method and the mirror-prox method.