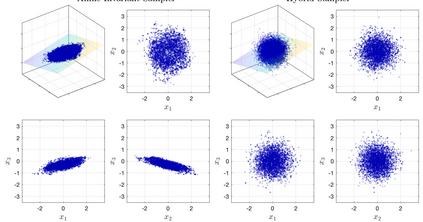
Sampling of sharp posteriors in high dimensions is a challenging problem, especially when gradients of the likelihood are unavailable. In low to moderate dimensions, affine-invariant methods, a class of ensemble-based gradient-free methods, have found success in sampling concentrated posteriors. However, the number of ensemble members must exceed the dimension of the unknown state in order for the correct distribution to be targeted. Conversely, the preconditioned Crank-Nicolson (pCN) algorithm succeeds at sampling in high dimensions, but samples become highly correlated when the posterior differs significantly from the prior. In this article we combine the above methods in two different ways as an attempt to find a compromise. The first method involves inflating the proposal covariance in pCN with that of the current ensemble, whilst the second performs approximately affine-invariant steps on a continually adapting low-dimensional subspace, while using pCN on its orthogonal complement.
翻译:在低度到中度的维度中,一种基于混合梯度的无梯度方法在抽样集中的后方方法中取得了成功。然而,混合成员的数量必须超过未知状态的维度,才能有针对性地进行正确分布。相反,具有先决条件的Crank-Nicolson(pCN)算法在高度取样中取得成功,但当后方与前方差异显著时,样本就变得高度相关。在本篇文章中,我们用两种不同的方式将上述方法结合起来,试图找到折中办法。第一种方法是将 pCN 提案的共变数与当前的共性建议相加,而第二种方法则在持续调整低维次空间时使用PCN 。