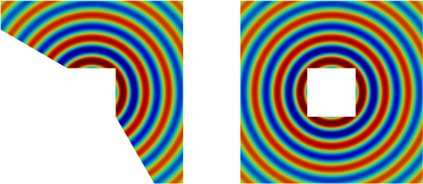
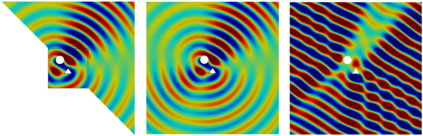
The Half-Space Matching (HSM) method has recently been developed as a new method for the solution of 2D scattering problems with complex backgrounds, providing an alternative to Perfectly Matched Layers (PML) or other artificial boundary conditions. Based on half-plane representations for the solution, the scattering problem is rewritten as a system of integral equations in which the unknowns are restrictions of the solution to the boundaries of a finite number of overlapping half-planes contained in the domain: this integral equation system is coupled to a standard finite element discretisation localised around the scatterer. While satisfactory numerical results have been obtained for real wavenumbers, wellposedness and equivalence to the original scattering problem have been established only for complex wavenumbers. In the present paper, by combining the HSM framework with a complex-scaling technique, we provide a new formulation for real wavenumbers which is provably well-posed and has the attraction for computation that the complex-scaled solutions of the integral equation system decay exponentially at infinity. The analysis requires the study of double-layer potential integral operators on intersecting infinite lines, and their analytic continuations. The effectiveness of the method is validated by preliminary numerical results.
翻译:半空间匹配方法(HSM)是最近开发的,作为解决具有复杂背景的2D散射问题的一种新方法,它为完全匹配的层或其他人工边界条件提供了替代物。根据半平方块对解决方案的表示,散射问题被改写成一个整体方程式系统,其中未知因素限制了对域内所含数量有限、重叠的半空平面界限的解决方案:这一整体方程式系统与分散器周围的局部化标准限定元素分解点相伴。虽然对实际波数、精密性和与原始散射问题等值的实际波数都取得了令人满意的数字结果,但只为复杂的波数设定了替代物。在本文件中,通过将HSM框架与复杂的伸缩技术相结合,我们为实际波数提供了一种新的配方,这种配方码的定位非常精准,并有吸引力来计算集成比例化的组合方程式系统复杂尺寸的溶解度,在无限的散射器周围以指数指数分解。分析需要研究双层潜在整体操作者对交错线进行初步验证。