Parameter-robust methods for the Biot-Stokes interfacial coupling without Lagrange multipliers

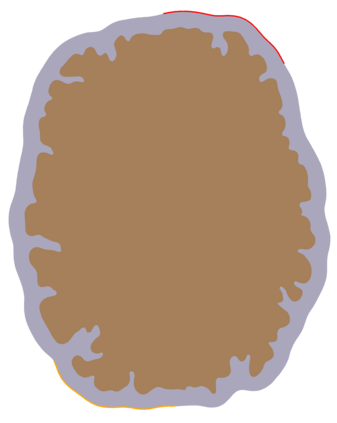
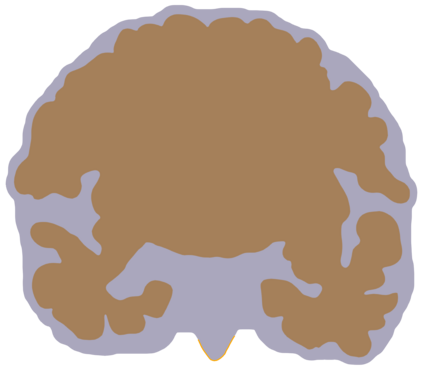
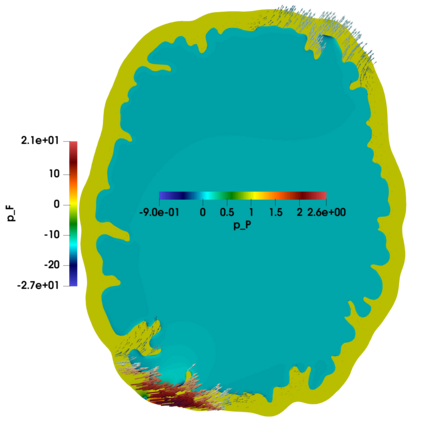
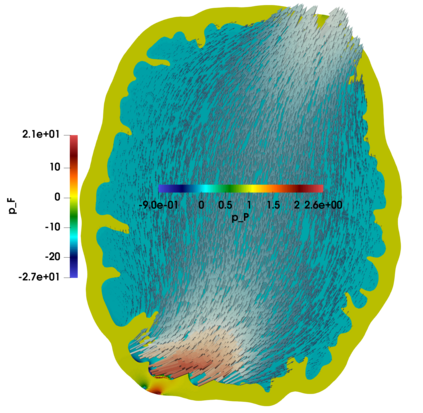
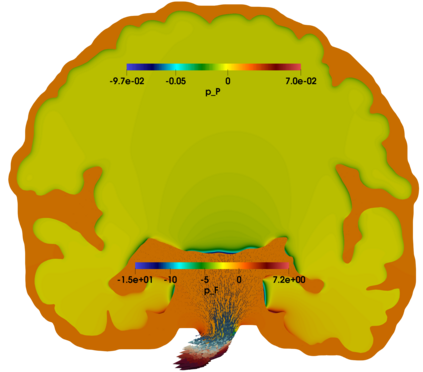
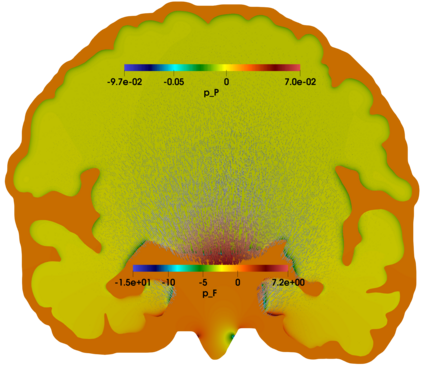
In this paper we advance the analysis of discretizations for a fluid-structure interaction model of the monolithic coupling between the free flow of a viscous Newtonian fluid and a deformable porous medium separated by an interface. A five-field mixed-primal finite element scheme is proposed solving for Stokes velocity-pressure and Biot displacement-total pressure-fluid pressure. Adequate inf-sup conditions are derived, and one of the distinctive features of the formulation is that its stability is established robustly in all material parameters. We propose robust preconditioners for this perturbed saddle-point problem using appropriately weighted operators in fractional Sobolev and metric spaces at the interface. The performance is corroborated by several test cases, including the application to interfacial flow in the brain.