On some variance reduction properties of the reparameterization trick

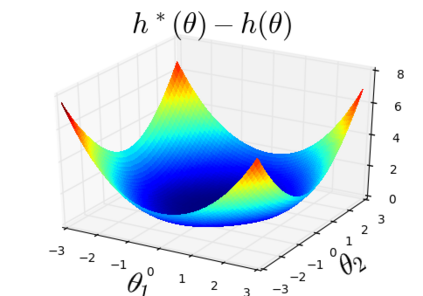
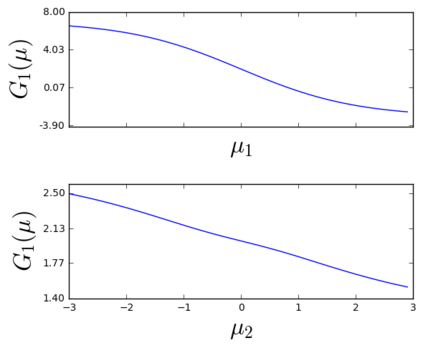
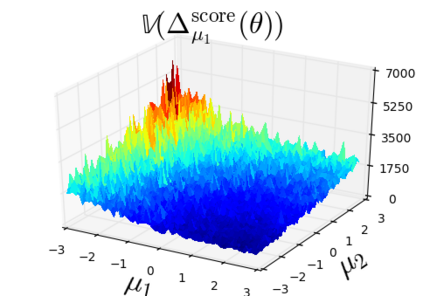
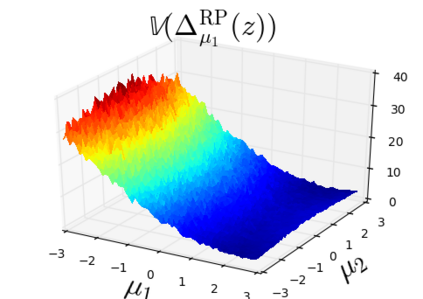
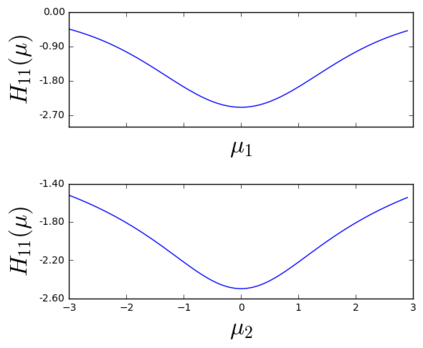
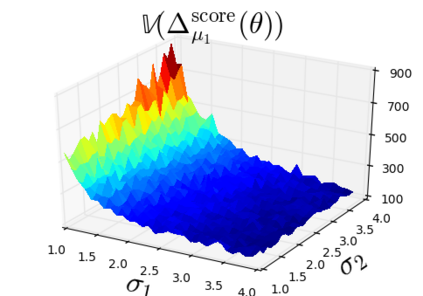
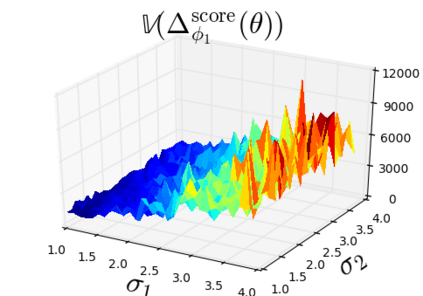
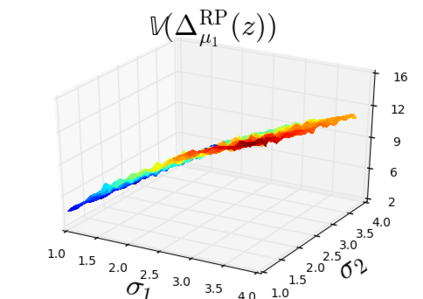
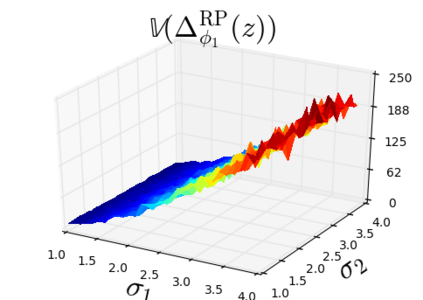
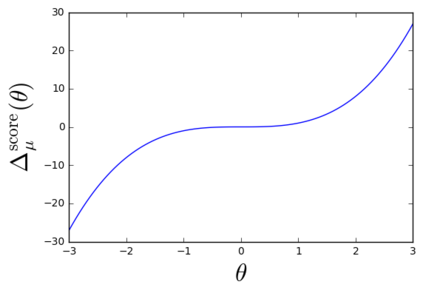
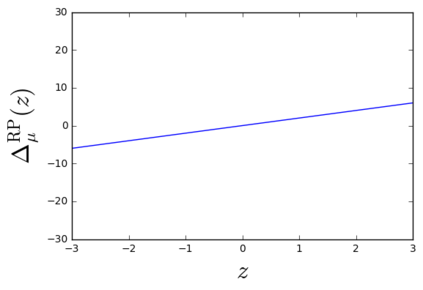
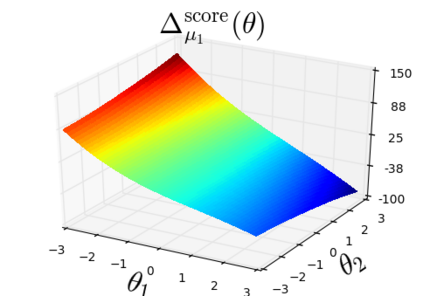
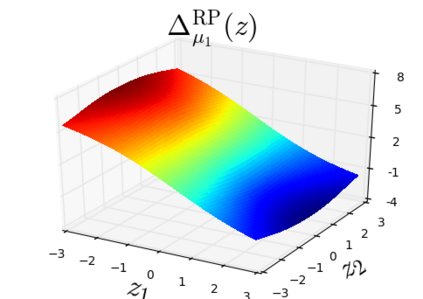
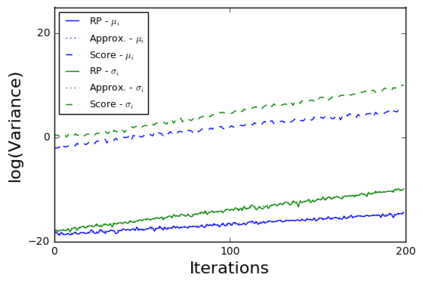
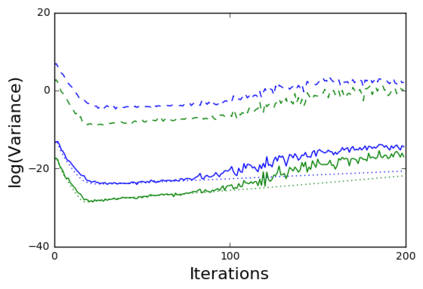
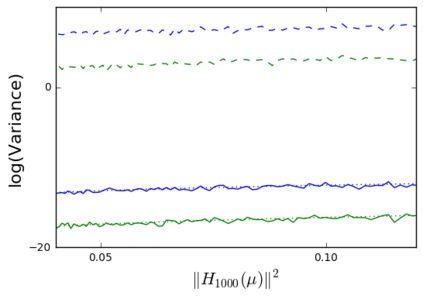
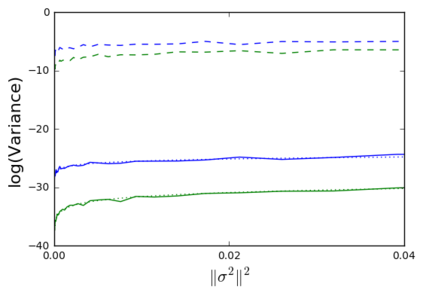
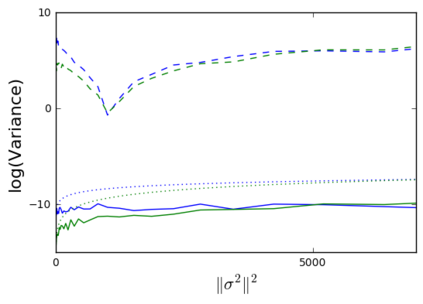
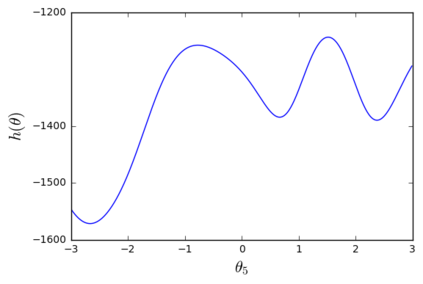
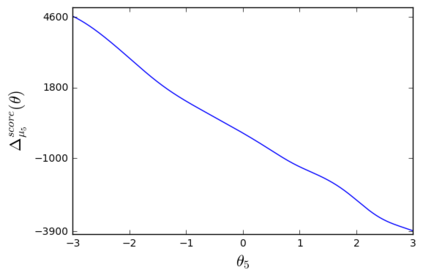
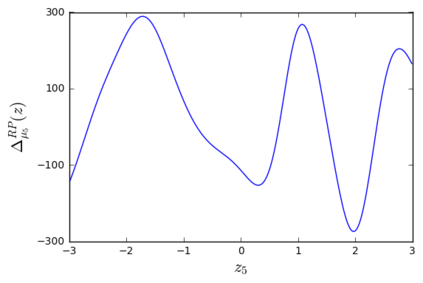
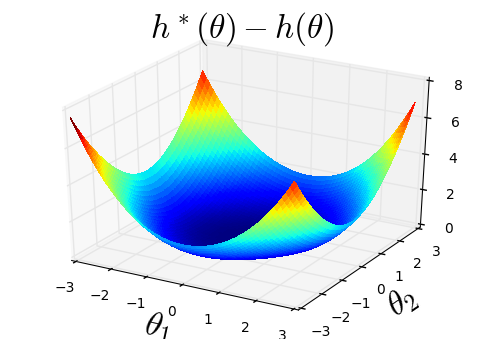
The so-called reparameterization trick is widely used in variational inference as it yields more accurate estimates of the gradient of the variational objective than alternative approaches such as the score function method. The resulting optimization converges much faster as the variance reduction offered by the reparameterization gradient is typically several orders of magnitude. There is overwhelming empirical evidence in the literature showing its success. However, there is relatively little research that explores why the reparameterization gradient is so effective. We explore this under two main simplifying assumptions. First, we assume that the variational approximation is the commonly used mean-field Gaussian density. Second, we assume that the log of the joint density of the model parameter vector and the data is a quadratic function that depends on the variational mean. These assumptions allow us to obtain tractable expressions for the marginal variances of the score function and reparameterization gradient estimators. We also derive lower bounds for the score function marginal variances through Rao-Blackwellization and prove that under our assumptions they are larger than those of the reparameterization trick. Finally, we apply the result of our idealized analysis to examples where the log-joint density is not quadratic, such as in a multinomial logistic regression and a Bayesian neural network with two layers.