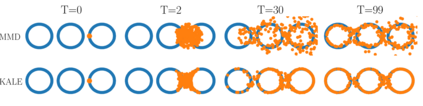
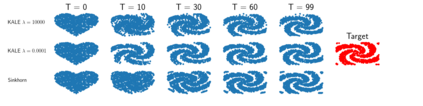
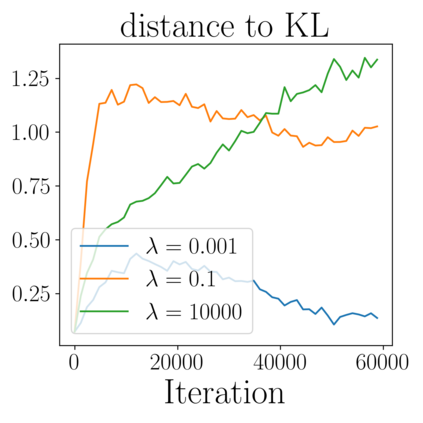
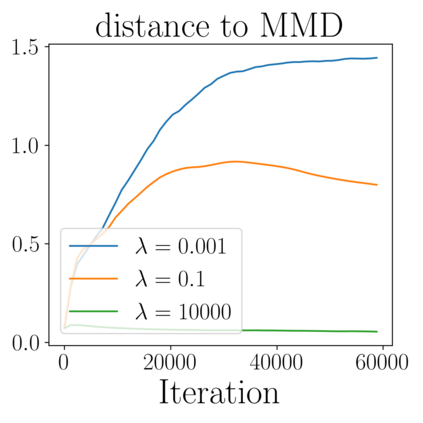
We study the gradient flow for a relaxed approximation to the Kullback-Leibler (KL) divergence between a moving source and a fixed target distribution. This approximation, termed the KALE (KL approximate lower-bound estimator), solves a regularized version of the Fenchel dual problem defining the KL over a restricted class of functions. When using a Reproducing Kernel Hilbert Space (RKHS) to define the function class, we show that the KALE continuously interpolates between the KL and the Maximum Mean Discrepancy (MMD). Like the MMD and other Integral Probability Metrics, the KALE remains well defined for mutually singular distributions. Nonetheless, the KALE inherits from the limiting KL a greater sensitivity to mismatch in the support of the distributions, compared with the MMD. These two properties make the KALE gradient flow particularly well suited when the target distribution is supported on a low-dimensional manifold. Under an assumption of sufficient smoothness of the trajectories, we show the global convergence of the KALE flow. We propose a particle implementation of the flow given initial samples from the source and the target distribution, which we use to empirically confirm the KALE's properties.
翻译:我们研究梯度流,以轻松接近移动源和固定目标分布之间的 Kullack- Leiber (KL) 移动源和固定目标分布之间的差值。 这个近值, 称为 KALE (KL 近似下下限估计值), 解决了Fenchel 双重问题的常规版本, 定义了功能等级的 KL。 当使用复制的 Kernel Hilbert 空间( RKHS) 来定义函数等级时, 我们显示 KALE 持续在 KLE 和 最大偏差( MMD) 之间进行交叉。 和 MMMD 和其他 综合概率分布模型一样, KALE 仍然被很好地定义为相异分布 。 尽管如此, KALE 相对于 MMD 来说, KLE, KLE 会继承限制 KLE 的对支持分布支持不匹配的敏感度。 这两个属性使得 KALE 梯度流在目标分布在低维方时特别适合。 在假设 KLE 轨迹足够平稳的情况下, 我们展示 KALE 流的全球趋同 。 我们提议从源和目标分布如何验证。