Some Statistic and Information-theoretic Results on Arithmetic Average Density Fusion

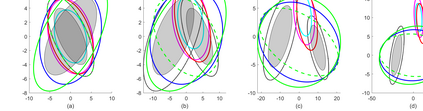
Finite mixture such as the Gaussian mixture is a flexible and powerful probabilistic modeling tool for representing the multimodal distribution widely involved in many estimation and learning problems. The core of it is representing the target distribution by the arithmetic average (AA) of a finite number of sub-distributions which constitute the mixture. The AA fusion has demonstrated compelling performance for both single-sensor and multi-sensor estimator design. In this paper, some statistic and information-theoretic results are given on the AA fusion approach, including its covariance consistency, mean square error, mode-preservation capacity, mixture information divergence and principles for fusing/mixing weight design. In particular, based on the concept of conservative fusion, the relationship of the AA fusion with the existing conservative fusion approaches such as covariance union and covariance intersection is exposed. The best fit of the mixture is formulated as a max-min problem, proving the sub-optimality of the AA fusion. Linear Gaussian models are considered for illustration and simulation comparison.