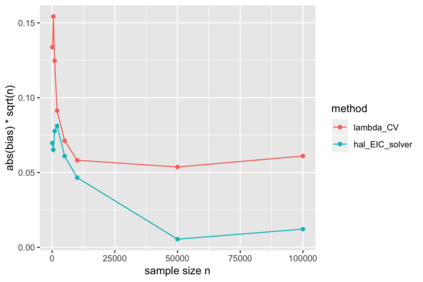
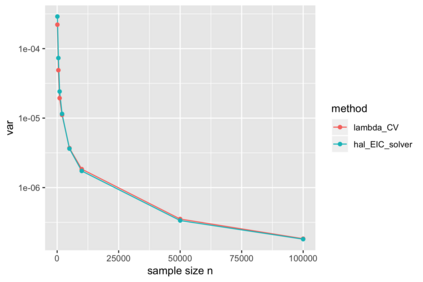
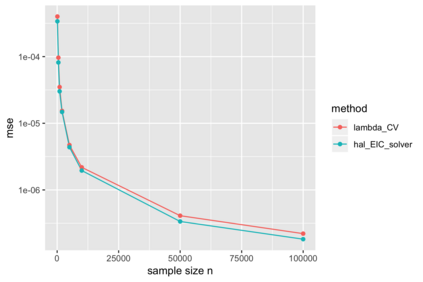
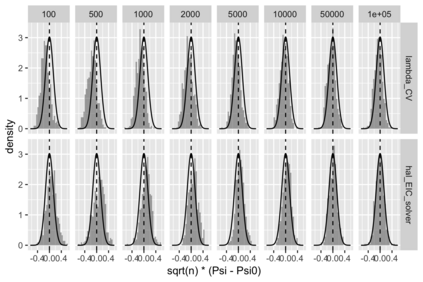
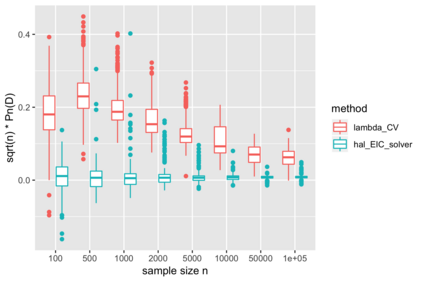
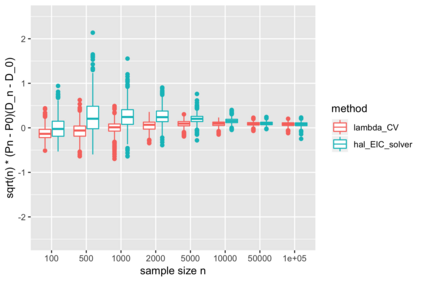
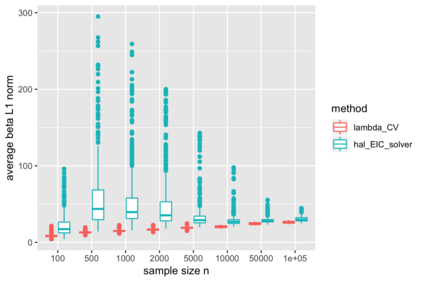
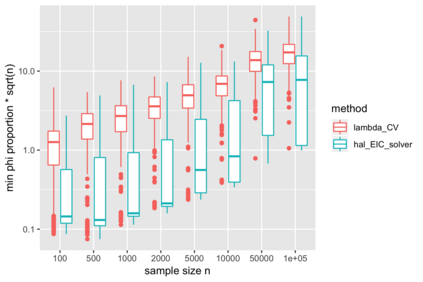
We consider estimation of a functional parameter of a realistically modeled data distribution based on observing independent and identically distributed observations. We define an $m$-th order Spline Highly Adaptive Lasso Minimum Loss Estimator (Spline HAL-MLE) of a functional parameter that is defined by minimizing the empirical risk function over an $m$-th order smoothness class of functions. We show that this $m$-th order smoothness class consists of all functions that can be represented as an infinitesimal linear combination of tensor products of $\leq m$-th order spline-basis functions, and involves assuming $m$-derivatives in each coordinate. By selecting $m$ with cross-validation we obtain a Spline-HAL-MLE that is able to adapt to the underlying unknown smoothness of the true function, while guaranteeing a rate of convergence faster than $n^{-1/4}$, as long as the true function is cadlag (right-continuous with left-hand limits) and has finite sectional variation norm. The $m=0$-smoothness class consists of all cadlag functions with finite sectional variation norm and corresponds with the original HAL-MLE defined in van der Laan (2015). In this article we establish that this Spline-HAL-MLE yields an asymptotically efficient estimator of any smooth feature of the functional parameter under an easily verifiable global undersmoothing condition. A sufficient condition for the latter condition is that the minimum of the empirical mean of the selected basis functions is smaller than a constant times $n^{-1/2}$, which is not parameter specific and enforces the selection of the $L_1$-norm in the lasso to be large enough to include sparsely supported basis. We demonstrate our general result for the $m=0$-HAL-MLE of the average treatment effect and of the integral of the square of the data density. We also present simulations for these two examples confirming the theory.
翻译:我们考虑根据独立和同样分布的观测,估算一个现实模型数据分布的功能参数。 我们定义了一个功能参数的美元顺序, 该功能参数的定义是:将实证风险功能在以美元顺序平滑性功能类别中的最低值最小化, 以观察独立和同样分布的观测为基础, 真实的模型数据分布的功能参数。 我们定义了一个功能参数的美元顺序: 高适应性高度激光最小值最小值最低值最低值最低值最低值最低值最高值最低值最低值最低值最低值最低值最低值最高值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值值值值值值最低值最低值值最低值最低值最低值值值值值值值值值值值值值, 最低值最低值最低值最低值最低值最低值值值最低值最低值值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值最低值