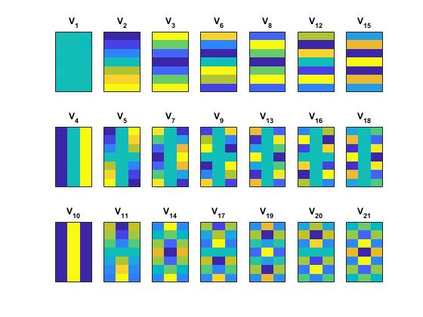
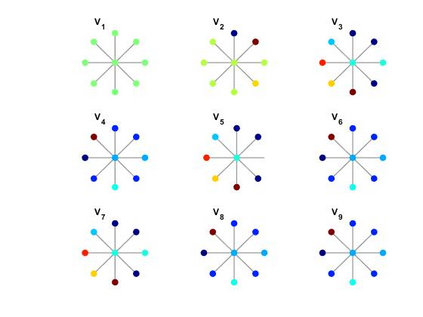
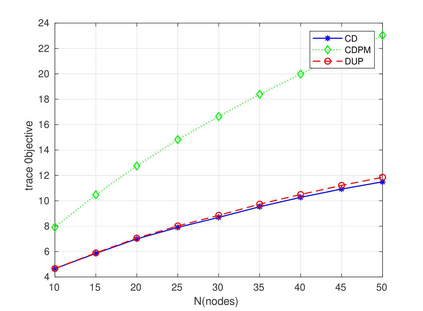
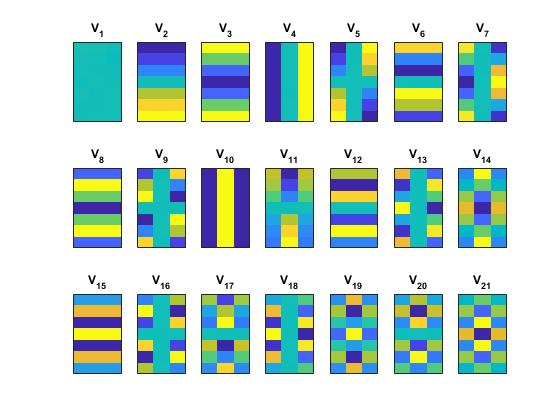
Graph signal processing uses the graph eigenvector basis to analyze signals. However, these graph eigenvectors are typically linearly ordered (by total variation), which may not be reasonable for many graph structures. There have been structure based similarity metrics proposed in the literature that better capture the geometry of graph eigenvectors. On the other hand, there has been work that attempts to generalize the concept of duality to graph signal processing. The (signal processing) the dual graph captures the relationship between graph frequencies and is obtained by typically inverting the graph Fourier transform operation. In this work, we investigate the connections between these two concepts. We propose a dualness measure of two graphs, which quantifies how close the graphs are being (signal processing) duals of each other. We show that this definition satisfies some desirable properties and develop an algorithm based on coordinate descent and perfect matching to compute an approximation to dualness. By computing the dualness measure, we observe that for structured graphs, the similarity metric-based techniques give a better dual graph (and vice-versa for ER graphs), suggesting a potentially novel approach unifying the two methods.
翻译:图形图示信号处理使用图示 egenvictor 来分析信号。 然而, 这些图示 egenvictors 通常是线性排列的( 完全变异的), 这对许多图形结构来说可能不合理。 文献中已经提出了基于结构的相似度量, 更好地捕捉图图egenvictors 的几何。 另一方面, 有工作试图将二元概念概括化为图示信号处理。 (信号处理) 双图捕捉了图形频率之间的关系, 并且通常通过倒转图Fourier 变换操作获得。 在此工作中, 我们研究了这两个概念之间的联系。 我们提出了两个图的双向度度度量度量, 以测量图形相互接近( 信号处理) 的两重度量度。 我们表明, 这个定义符合某些理想的属性, 并开发一种基于协调血统和完美匹配的算法, 以将近似值与二元性进行计算。 我们观察到, 对于结构化的图形来说, 相似的衡量技术提供了一种更好的双向图形( 和ER 图表的反向), 表示一种可能的新方法 。