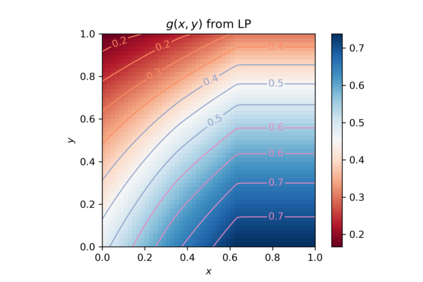
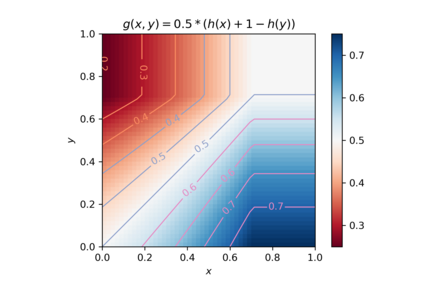
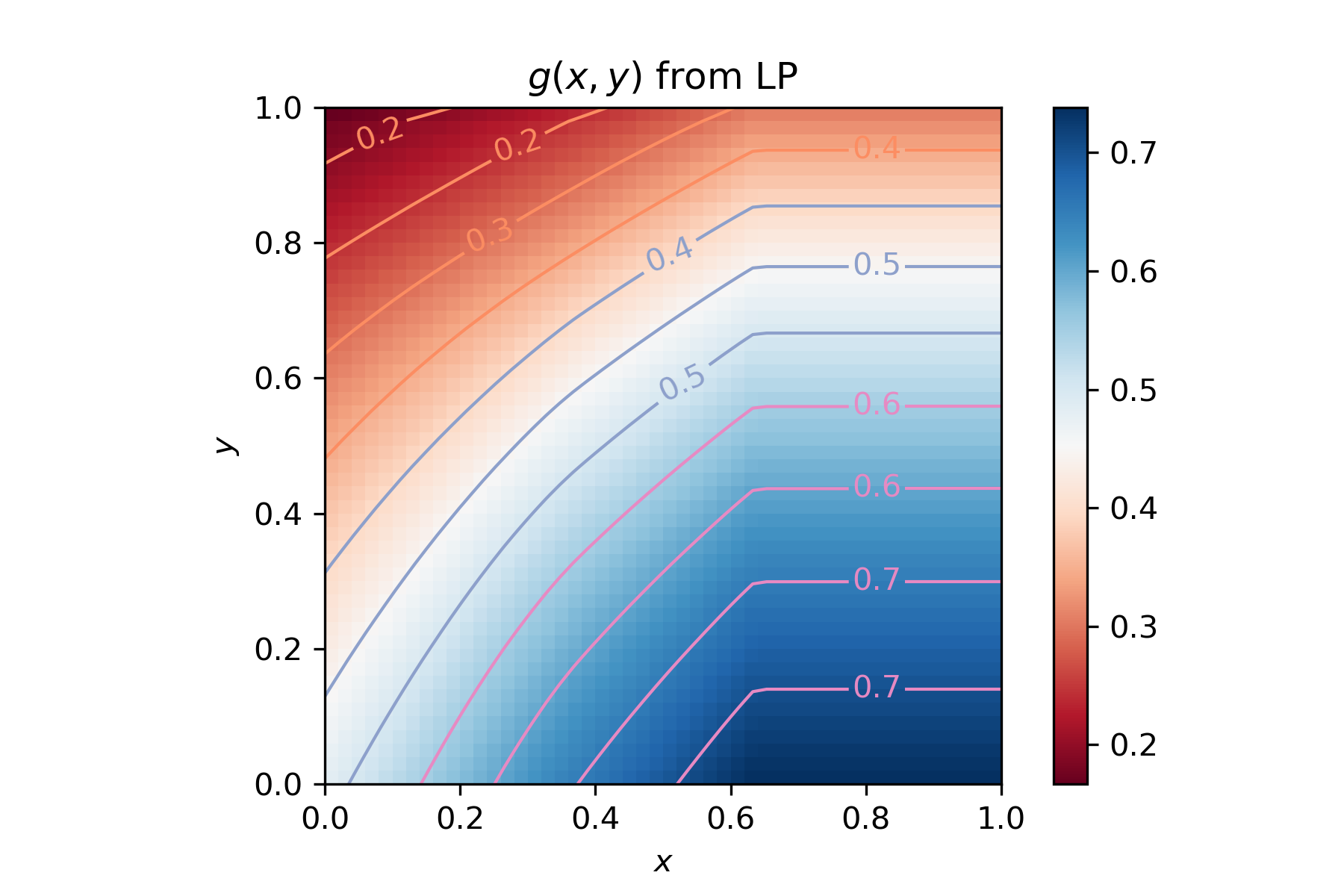
In this paper, we consider the online vertex-weighted bipartite matching problem in the random arrival model. We consider the generalization of the RANKING algorithm for this problem introduced by Huang, Tang, Wu, and Zhang (TALG 2019), who show that their algorithm has a competitive ratio of 0.6534. We show that assumptions in their analysis can be weakened, allowing us to replace their derivation of a crucial function $g$ on the unit square with a linear program that computes the values of a best possible $g$ under these assumptions on a discretized unit square. We show that the discretization does not incur much error, and show computationally that we can obtain a competitive ratio of 0.6629. To compute the bound over our discretized unit square we use parallelization, and still needed two days of computing on a 64-core machine. Furthermore, by modifying our linear program somewhat, we can show computationally an upper bound on our approach of 0.6688; any further progress beyond this bound will require either further weakening in the assumptions of $g$ or a stronger analysis than that of Huang et al.
翻译:在本文中,我们考虑了随机抵达模型中的在线顶端加权双边匹配问题。我们考虑了黄、唐、吴和张(TALG 2019)为这一问题引入的RANKking算法(TALG 2019)的概括化,后者显示其算法的竞争性比率为0.6534。我们表明,其分析中的假设可以被削弱,让我们用一个线性程序来取代单位方形上一个关键函数g$g的衍生法,用线性程序计算出在离散单位方形上这些假设下可能最佳的g美元值。我们表明,离散化没有多大的错误,并用计算显示我们可以得到0.6629的竞争性比率,以计算我们使用平行法的分解单位方形的界限,仍然需要两天在64个核心机上进行计算。此外,通过修改我们的线性程序,我们可以以0.6688的计算法上一个上限;超出这一界限的任何进一步的进展都需要在美元假设中进一步削弱,或者比对黄等人进行更强的分析。