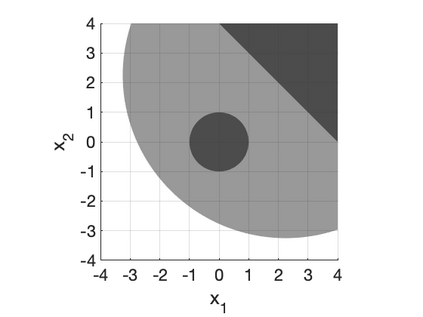
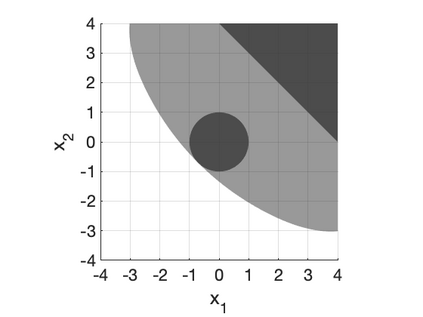
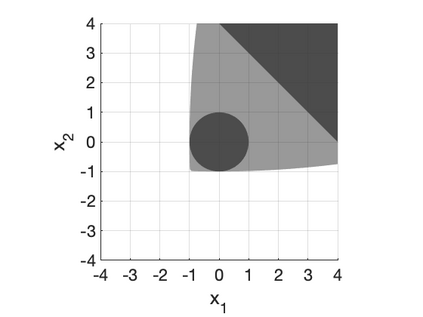
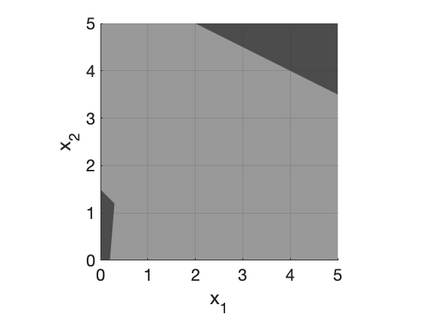
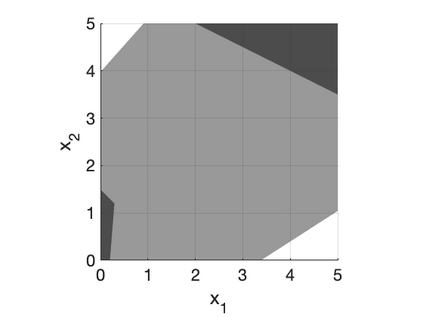
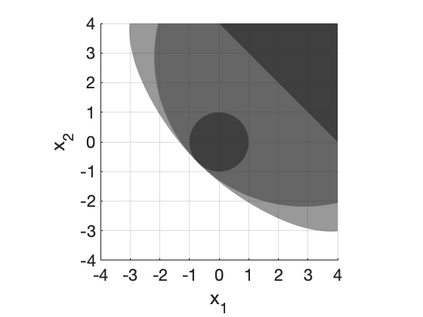
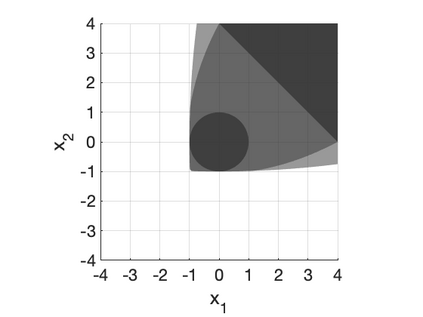
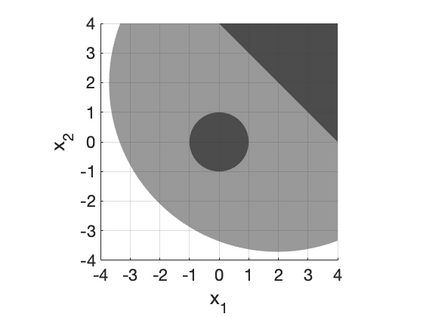
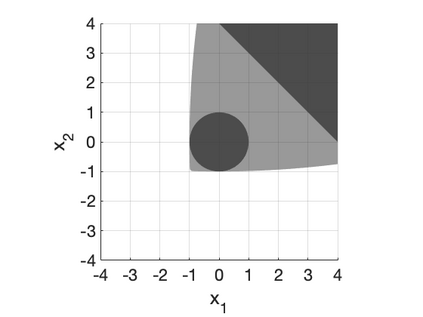
We develop a class of mixed-integer formulations for disjunctive constraints intermediate to the big-M and convex hull formulations in terms of relaxation strength. The main idea is to capture the best of both the big-M and convex hull formulations: a computationally light formulation with a tight relaxation. The "$P$-split" formulations are based on a lifted transformation that splits convex additively separable constraints into $P$ partitions and forms the convex hull of the linearized and partitioned disjunction. We analyze the continuous relaxation of the $P$-split formulations and show that, under certain assumptions, the formulations form a hierarchy starting from a big-M equivalent and converging to the convex hull. The goal of the $P$-split formulations is to form a strong approximation of the convex hull through a computationally simpler formulation. We computationally compare the $P$-split formulations against big-M and convex hull formulations on 320 test instances. The test problems include K-means clustering, P_ball problems, and optimization over trained ReLU neural networks. The computational results show promising potential of the $P$-split formulations. For many of the test problems, $P$-split formulations are solved with a similar number of explored nodes as the convex hull formulation, while reducing the solution time by an order of magnitude and outperforming big-M both in time and number of explored nodes.
翻译:我们开发了一种混合整形配方,用于与大M型和软壳体配方的分流性限制,中间是大M型和软体配方,主要想法是捕捉大M型和软体配方的最佳配方:一种计算式的光度配方,紧松放松。“$P$分裂”配方的基础是一种解除式的转换,它将锥形的分解成美元和分解型的分流体的分流体。我们在320次测试中,我们分析了美元分流的配方的持续放松情况,并表明在某些假设下,这些配方构成一种等级,从大M型和软体配方体的等量和凝聚体配方的分级。 $-P$配方的分流体组合、P_球型配方的分流体组合和分流体的分流体型体配制,测试问题包括K-单位-美元分制的组合、在类似制式的折体制型中,在模拟的折体制式中,测试结果显示的分流体型的分流的分解。