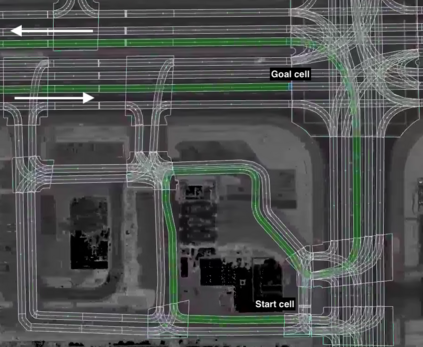
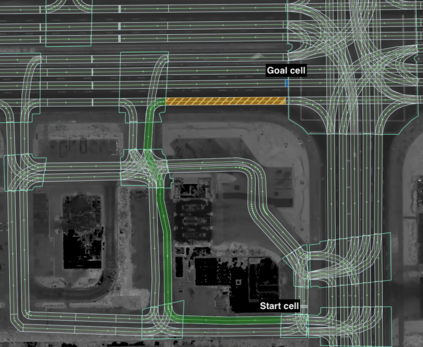
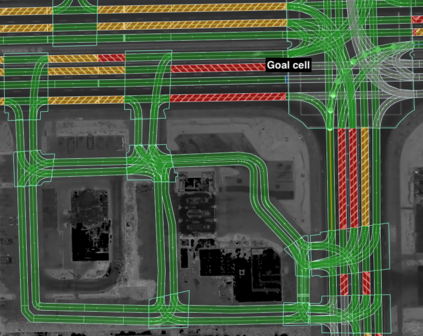
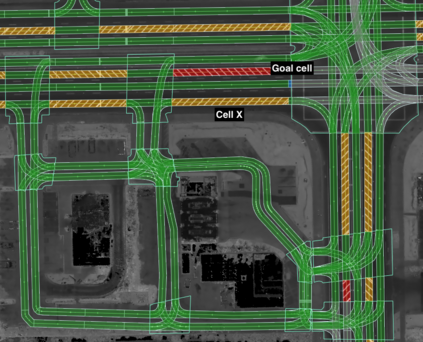
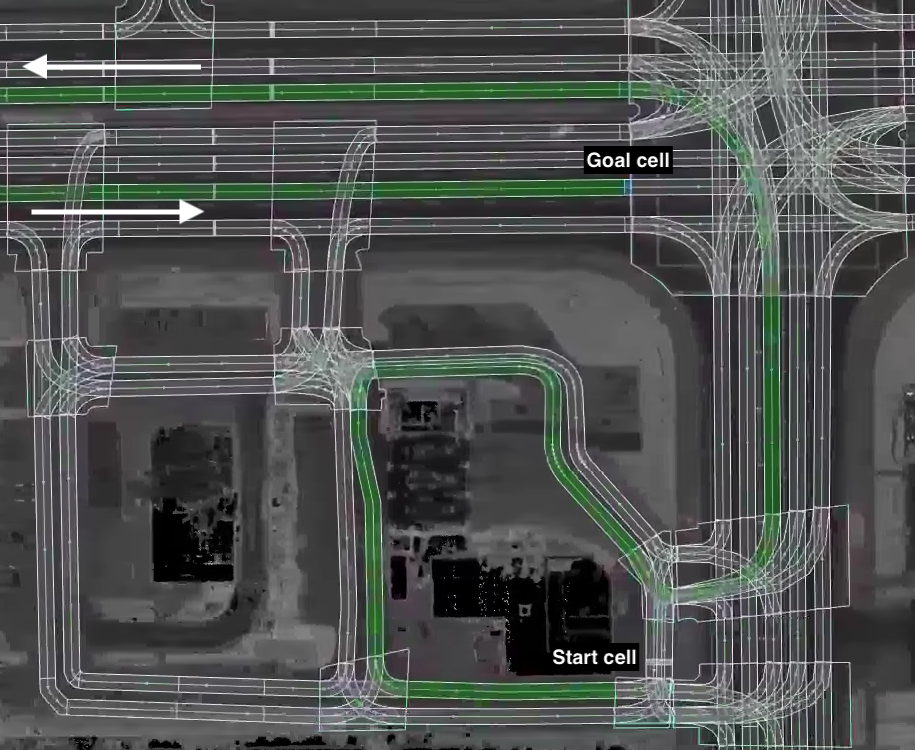
We present an algorithm that, given a representation of a road network in lane-level detail, computes a route that minimizes the expected cost to reach a given destination. In doing so, our algorithm allows us to solve for the complex trade-offs encountered when trying to decide not just which roads to follow, but also when to change between the lanes making up these roads, in order to -- for example -- reduce the likelihood of missing a left exit while not unnecessarily driving in the leftmost lane. This routing problem can naturally be formulated as a Markov Decision Process (MDP), in which lane change actions have stochastic outcomes. However, MDPs are known to be time-consuming to solve in general. In this paper, we show that -- under reasonable assumptions -- we can use a Dijkstra-like approach to solve this stochastic problem, and benefit from its efficient $O(n \log n)$ running time. This enables an autonomous vehicle to exhibit lane-selection behavior as it efficiently plans an optimal route to its destination.
翻译:暂无翻译