A Post-Quantum Key Agreement Protocol Based on a Modified Matrix-Power Function over a Rectangular Matrices Semiring

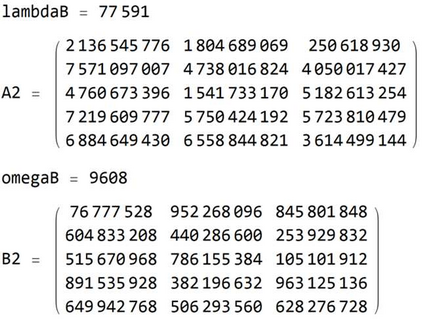
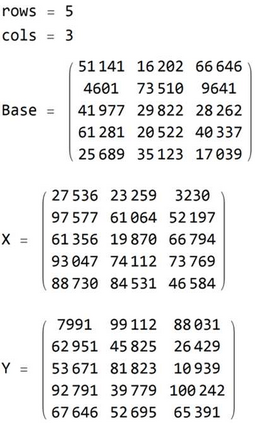
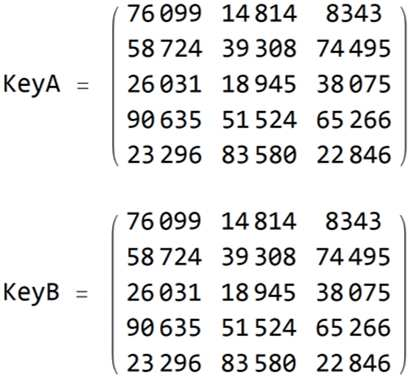
We present an improved post-quantum version of Sakalauskas matrix power function key-agreement protocol, using rectangular matrices instead the original square ones. Sakalauskas matrix power function is an efficient and secure way to generate a shared secret key, and using rectangular matrices can provide additional flexibility and security in some applications. This method reduces the computational complexity by allowing smaller random integers matrices while maintaining equal security. Another advantage of using the rank-deficient rectangular matrices over key agreement protocols is that it provides more protection against several linearization attacks.