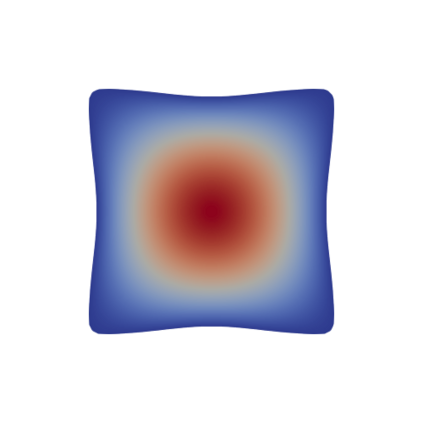
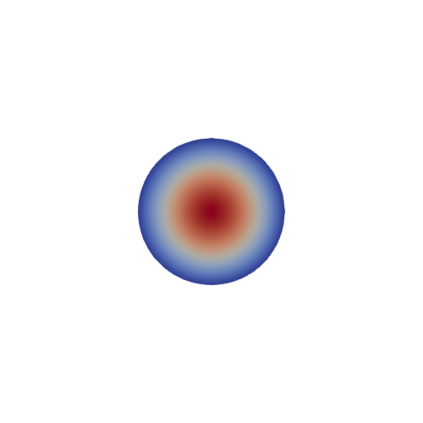
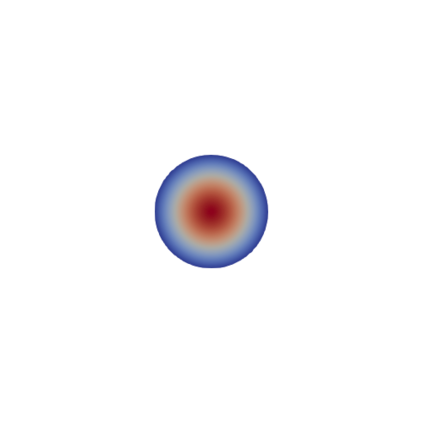
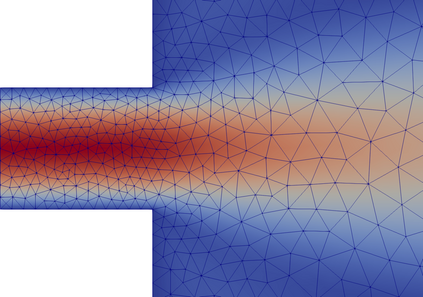
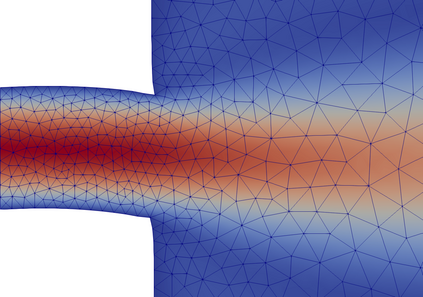
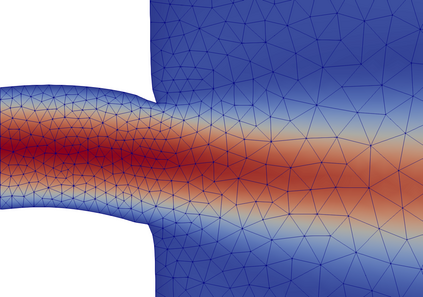
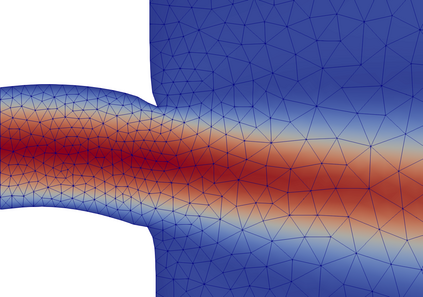
Many problems in engineering can be understood as controlling the bifurcation structure of a given device. For example, one may wish to delay the onset of instability, or bring forward a bifurcation to enable rapid switching between states. We propose a numerical technique for controlling the bifurcation diagram of a nonlinear partial differential equation by varying the shape of the domain. Specifically, we are able to delay or advance a given branch point to a target parameter value. The algorithm consists of solving a shape optimization problem constrained by an augmented system of equations, the Moore--Spence system, that characterize the location of the branch points. Numerical experiments on the Allen--Cahn, Navier--Stokes, and hyperelasticity equations demonstrate the effectiveness of this technique in a wide range of settings.
翻译:工程中的许多问题可以被理解为控制给定装置的双向结构。 例如, 人们可能希望推迟不稳定的开始, 或者提出两向以允许各州之间的快速转换。 我们提出一个数字技术来通过改变域的形状来控制非线性部分方程式的双向图。 具体地说, 我们能够将给定的分支点延迟或推进到目标参数值。 算法包括解决一个受扩大的方程式系统摩尔- 思朋斯系统制约的形状优化问题, 该系统是分支点位置的特征。 Allen- Cahn、 Navier- Stokes 和超弹性方程式的数值实验显示了该技术在广泛环境中的有效性 。