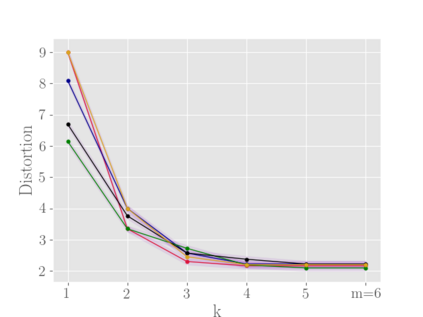
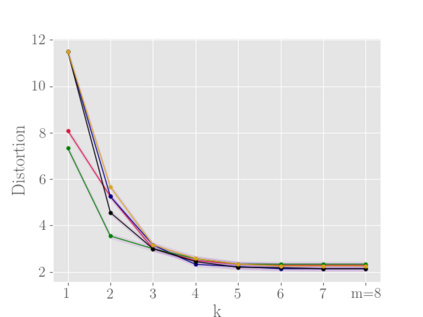
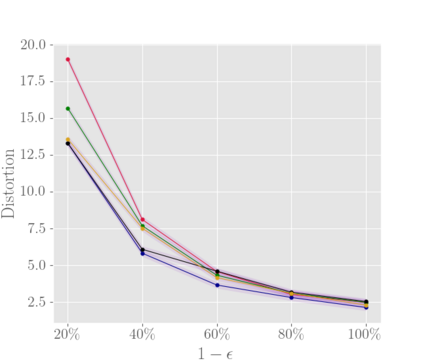
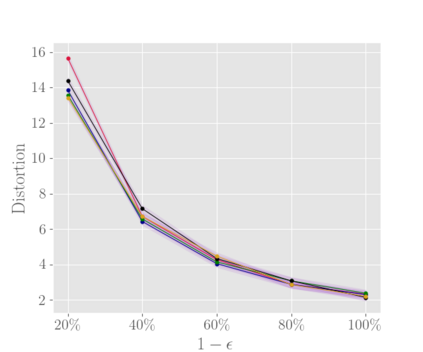
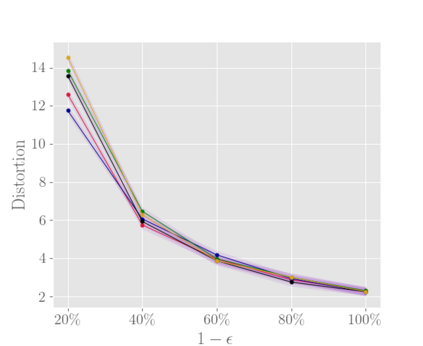
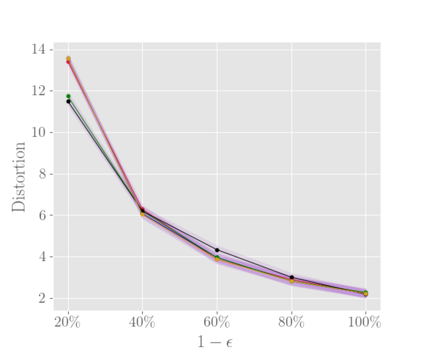
In this work we study the metric distortion problem in voting theory under a limited amount of ordinal information. Our primary contribution is threefold. First, we consider mechanisms which perform a sequence of pairwise comparisons between candidates. We show that a widely-popular deterministic mechanism employed in most knockout phases yields distortion $\mathcal{O}(\log m)$ while eliciting only $m-1$ out of $\Theta(m^2)$ possible pairwise comparisons, where $m$ represents the number of candidates. Our analysis for this mechanism leverages a powerful technical lemma recently developed by Kempe \cite{DBLP:conf/aaai/000120a}. We also provide a matching lower bound on its distortion. In contrast, we prove that any mechanism which performs fewer than $m-1$ pairwise comparisons is destined to have unbounded distortion. Moreover, we study the power of deterministic mechanisms under incomplete rankings. Most notably, when every agent provides her $k$-top preferences we show an upper bound of $6 m/k + 1$ on the distortion, for any $k \in \{1, 2, \dots, m\}$. Thus, we substantially improve over the previous bound of $12 m/k$ recently established by Kempe \cite{DBLP:conf/aaai/000120a,DBLP:conf/aaai/000120b}, and we come closer to matching the best-known lower bound. Finally, we are concerned with the sample complexity required to ensure near-optimal distortion with high probability. Our main contribution is to show that a random sample of $\Theta(m/\epsilon^2)$ voters suffices to guarantee distortion $3 + \epsilon$ with high probability, for any sufficiently small $\epsilon > 0$. This result is based on analyzing the sensitivity of the deterministic mechanism introduced by Gkatzelis, Halpern, and Shah \cite{DBLP:conf/focs/Gkatzelis0020}. Importantly, all of our sample-complexity bounds are distribution-independent.
翻译:在这项工作中,我们根据数量有限的普通信息来研究120美元投票理论中的标准扭曲问题。 我们的主要贡献是三倍。 首先, 我们考虑在候选人之间进行一系列对称比较的机制。 我们显示, 在多数淘汰阶段使用的广受欢迎的确定性机制可以产生扭曲 $mathcal{O}(logm)$(log m), 而仅仅从$@Teta(m%2) 中得出1美元-1美元, 其中20美元代表候选人的数量。 我们对于这个机制的分析利用了由 Kempe\cite: DBLP:conf/aaaai/000120a}最近开发的一个强大的技术利玛。 相比之下, 我们证明, 任何执行低于$-1美元的对立度比较的机制都注定不会受到扭曲。 此外, 我们研究在排名不完全的情况下, 确定 美元/ 美元机制的力量。 最明显的是, 当每个代理提供美元和最清楚的偏好的信息偏好时, 我们显示一个6 m/k+1美元的上层, 更接近扭曲, 美元- m\\\\ m=x ml