Compressed Sensing: A Discrete Optimization Approach

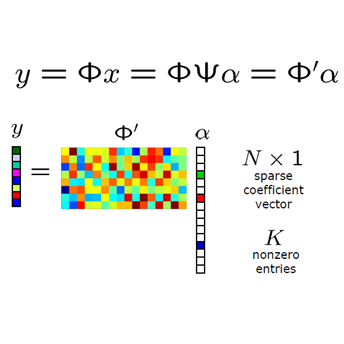
We study the Compressed Sensing (CS) problem, which is the problem of finding the most sparse vector that satisfies a set of linear measurements up to some numerical tolerance. We introduce an $\ell_2$ regularized formulation of CS which we reformulate as a mixed integer second order cone program. We derive a second order cone relaxation of this problem and show that under mild conditions on the regularization parameter, the resulting relaxation is equivalent to the well studied basis pursuit denoising problem. We present a semidefinite relaxation that strengthens the second order cone relaxation and develop a custom branch-and-bound algorithm that leverages our second order cone relaxation to solve small-scale instances of CS to certifiable optimality. When compared against solutions produced by three state of the art benchmark methods on synthetic data, our numerical results show that our approach produces solutions that are on average $6.22\%$ more sparse. When compared only against the experiment-wise best performing benchmark method on synthetic data, our approach produces solutions that are on average $3.10\%$ more sparse. On real world ECG data, for a given $\ell_2$ reconstruction error our approach produces solutions that are on average $9.95\%$ more sparse than benchmark methods ($3.88\%$ more sparse if only compared against the best performing benchmark), while for a given sparsity level our approach produces solutions that have on average $10.77\%$ lower reconstruction error than benchmark methods ($1.42\%$ lower error if only compared against the best performing benchmark). When used as a component of a multi-label classification algorithm, our approach achieves greater classification accuracy than benchmark compressed sensing methods. This improved accuracy comes at the cost of an increase in computation time by several orders of magnitude.