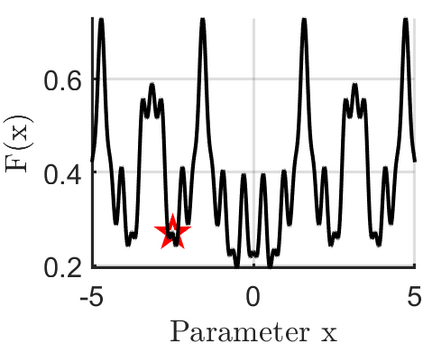
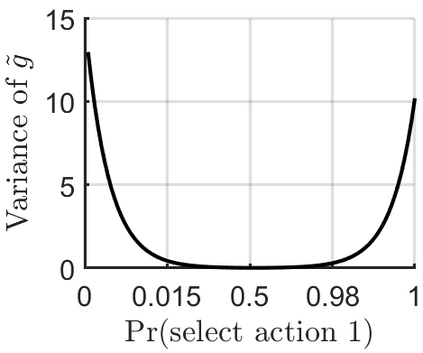
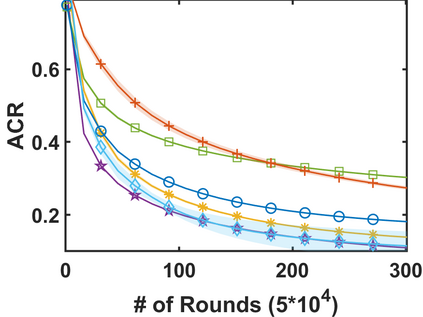
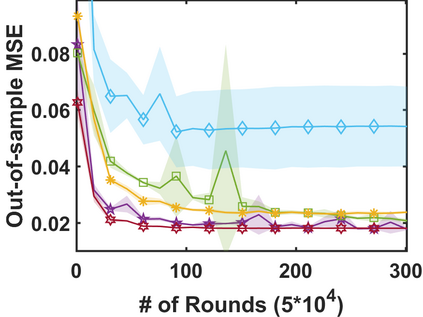
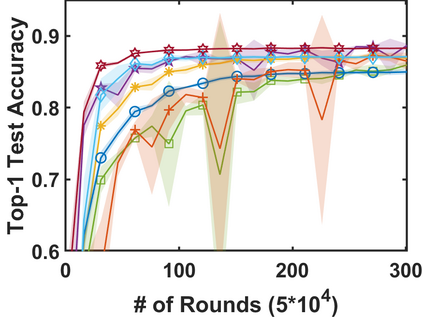
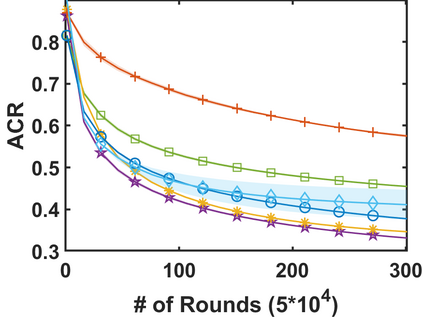
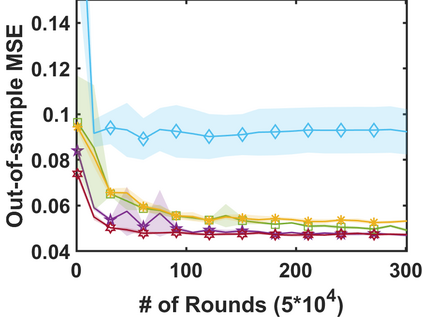
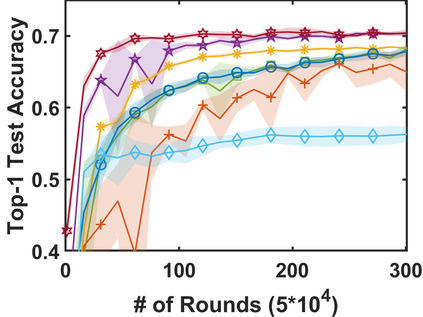
In stochastic contextual bandit (SCB) problems, an agent selects an action based on certain observed context to maximize the cumulative reward over iterations. Recently there have been a few studies using a deep neural network (DNN) to predict the expected reward for an action, and the DNN is trained by a stochastic gradient based method. However, convergence analysis has been greatly ignored to examine whether and where these methods converge. In this work, we formulate the SCB that uses a DNN reward function as a non-convex stochastic optimization problem, and design a stage-wise stochastic gradient descent algorithm to optimize the problem and determine the action policy. We prove that with high probability, the action sequence chosen by this algorithm converges to a greedy action policy respecting a local optimal reward function. Extensive experiments have been performed to demonstrate the effectiveness and efficiency of the proposed algorithm on multiple real-world datasets.
翻译:在切分背景土匪(SCB)问题中,代理商根据观察到的某些背景选择一项行动,以最大限度地增加迭代的累积奖赏。最近进行了几项研究,利用深神经网络(DNN)来预测一项行动的预期奖赏,DNN则通过一种随机切分梯度法培训。然而,趋同分析被严重忽略,以检查这些方法是否和在哪里汇合。在这项工作中,我们制定了SCB,将DNN奖赏功能作为非convex蒸馏力优化问题,并设计了一种分阶段的随机随机梯度梯度下限算法,以优化问题并确定行动政策。我们证明,这一算法所选择的行动序列极有可能与关于当地最佳奖赏功能的贪婪行动政策汇合在一起。我们进行了广泛的实验,以证明多种真实世界数据集的拟议算法的有效性和效率。