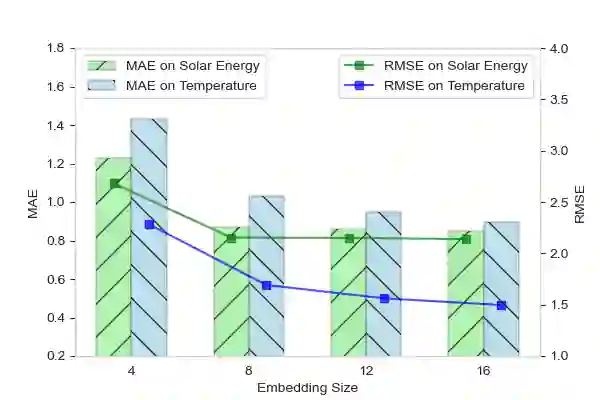
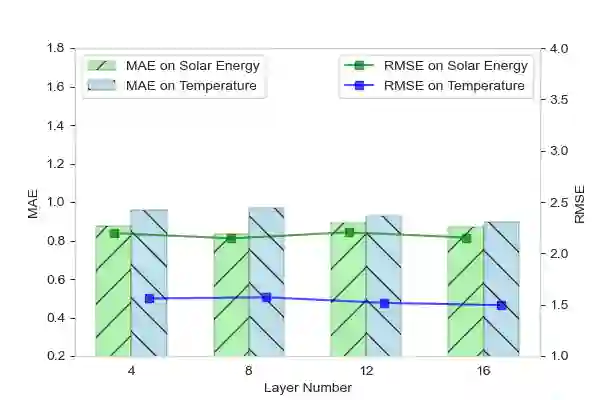
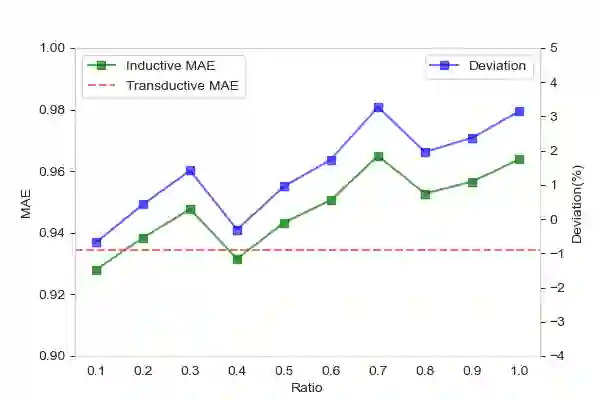
Graph-based spatio-temporal neural networks are effective to model the spatial dependency among discrete points sampled irregularly from unstructured grids, thanks to the great expressiveness of graph neural networks. However, these models are usually spatially-transductive -- only fitting the signals for discrete spatial nodes fed in models but unable to generalize to `unseen' spatial points with zero-shot. In comparison, for forecasting tasks on continuous space such as temperature prediction on the earth's surface, the \textit{spatially-inductive} property allows the model to generalize to any point in the spatial domain, demonstrating models' ability to learn the underlying mechanisms or physics laws of the systems, rather than simply fit the signals. Besides, in temporal domains, \textit{irregularly-sampled} time series, e.g. data with missing values, urge models to be temporally-continuous. Motivated by the two issues, we propose a spatio-temporal framework based on neural operators for PDEs, which learn the underlying mechanisms governing the dynamics of spatially-continuous physical quantities. Experiments show our model's improved performance on forecasting spatially-continuous physic quantities, and its superior generalization to unseen spatial points and ability to handle temporally-irregular data.
翻译:以图形为基础的空间时空神经网络能够有效地模拟从非结构化电网中不定期抽样的离散点之间的空间依赖性,这归功于图形神经网络的高度清晰度。然而,这些模型通常都是空间传输的 -- -- 仅适合在模型中输入的离散空间节点的信号,但无法以零发数概括“不见”空间点。相比之下,对于连续空间的预测任务,如地球表面的温度预测等,由于Textit{spative- intionive}属性使得模型能够向空间域中的任何点推广,展示模型学习系统基本机制或物理定律的能力,而不仅仅是适应信号。此外,在时空域中,\textit{不定期抽样}时间序列,例如缺少值的数据,敦促模型保持时间的连续性。受这两个问题驱动,我们提议了一个基于PDE模型神经操作器的空基框架,用以展示模型学习管理其空间空间空间空间预测的高级空间动态、空间空间预测能力的高级机制,以显示其空间空间空间-空间-空间-空间-空间-持续变化的物理特性。