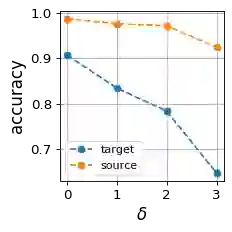
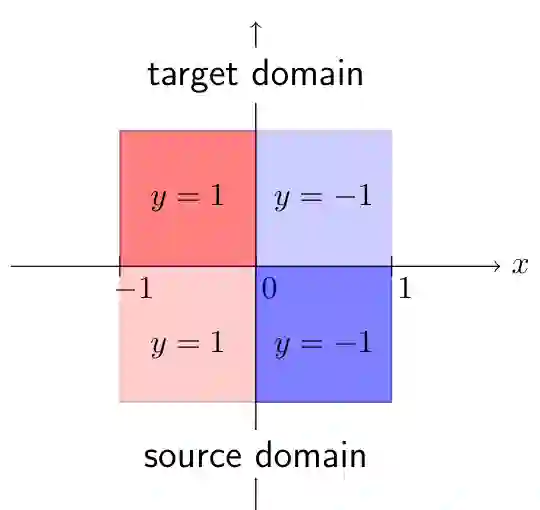
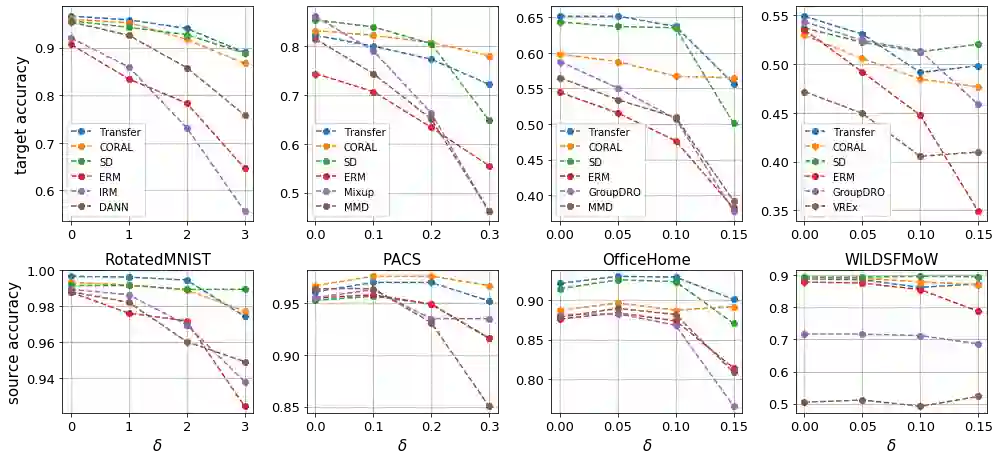
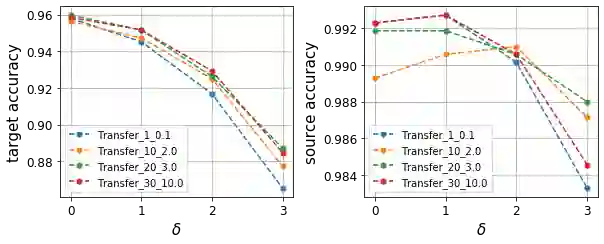
Out-of-distribution generalization is one of the key challenges when transferring a model from the lab to the real world. Existing efforts mostly focus on building invariant features among source and target domains. Based on invariant features, a high-performing classifier on source domains could hopefully behave equally well on a target domain. In other words, the invariant features are \emph{transferable}. However, in practice, there are no perfectly transferable features, and some algorithms seem to learn ''more transferable'' features than others. How can we understand and quantify such \emph{transferability}? In this paper, we formally define transferability that one can quantify and compute in domain generalization. We point out the difference and connection with common discrepancy measures between domains, such as total variation and Wasserstein distance. We then prove that our transferability can be estimated with enough samples and give a new upper bound for the target error based on our transferability. Empirically, we evaluate the transferability of the feature embeddings learned by existing algorithms for domain generalization. Surprisingly, we find that many algorithms are not quite learning transferable features, although few could still survive. In light of this, we propose a new algorithm for learning transferable features and test it over various benchmark datasets, including RotatedMNIST, PACS, Office-Home and WILDS-FMoW. Experimental results show that the proposed algorithm achieves consistent improvement over many state-of-the-art algorithms, corroborating our theoretical findings.
翻译:将模型从实验室转移到真实世界时, 分配上的一般化是关键挑战之一。 现有的努力主要侧重于在源域和目标域间建立差异性特征。 基于变量性特征, 源域上高性分类者有望在目标域内同样表现良好。 换句话说, 差异性特征是可转移性的。 然而, 实际上, 没有完全可转让性, 一些算法似乎学习到“ 更可转让性” 特征。 我们如何理解和量化这种\emph{ 可转让性? 在本文中, 我们正式定义了可转让性, 从而可以量化和解析源域常规化。 我们指出, 源域间高性分类器在目标域间, 如全变异性和瓦塞斯坦距离等, 可以同样地运行。 我们然后证明, 我们的可转让性特征可以用足够样本来估计, 并且根据我们的可转移性对目标错误给予新的上限。 我们很生的, 我们评估了从现有的域化通用算法中学习的许多特性的可传递性嵌化性。 令人惊讶的是, 我们发现许多的逻辑性算算法是相当易变的,, 。 我们的轨性变化的路径性变化的特性可以显示,, 我们的路径性数据比的路径性数据基化的特性比的比比的比的路径性, 。