Extended Unconstrained Features Model for Exploring Deep Neural Collapse

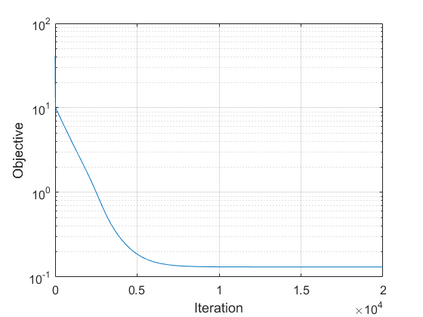
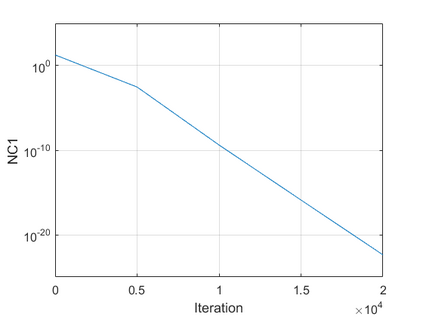
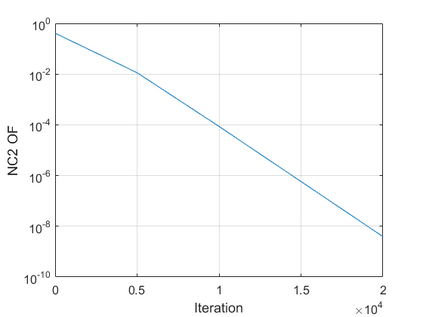
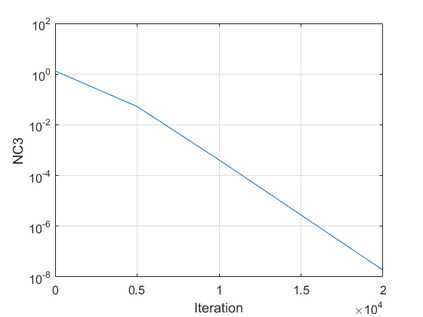
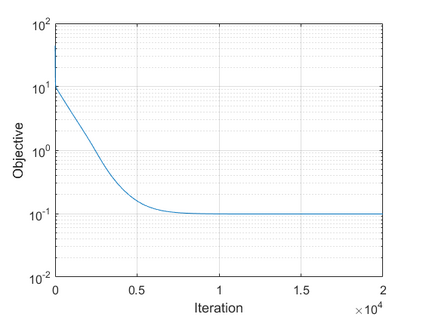
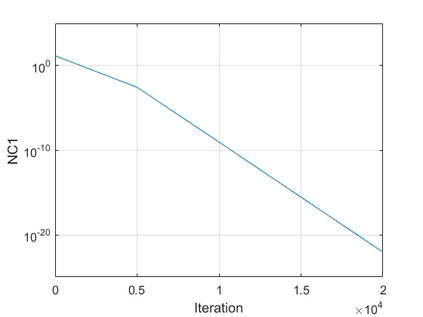
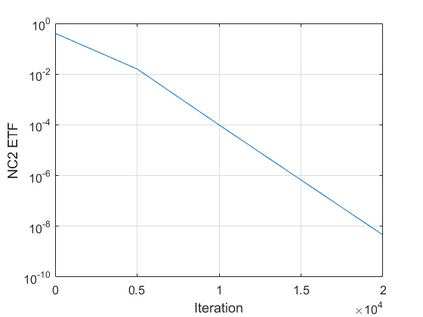
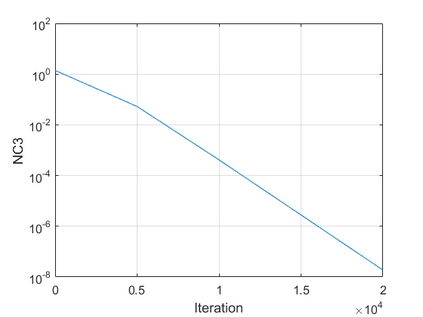
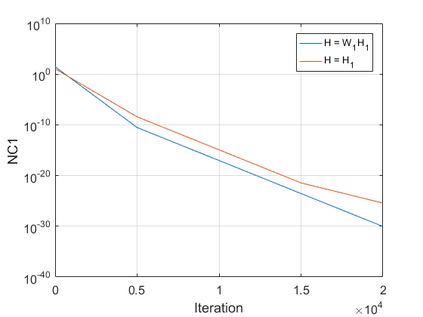
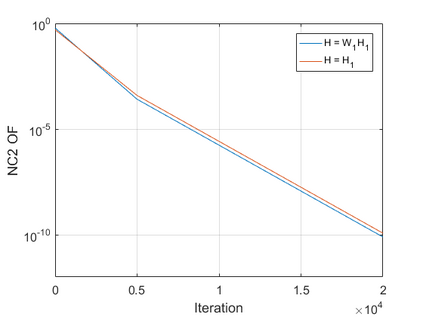
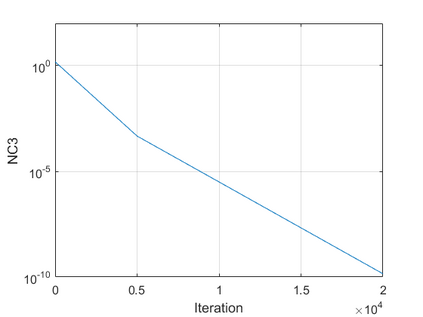
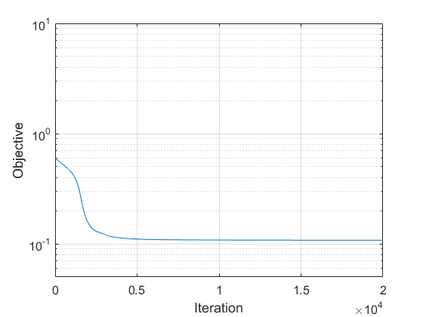
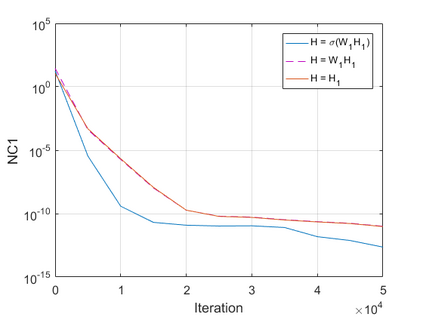
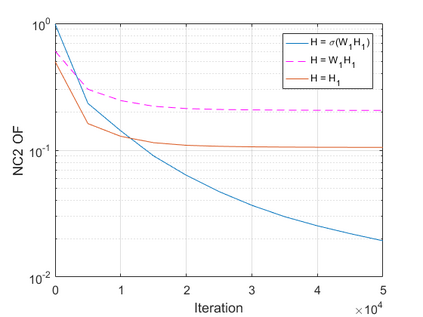
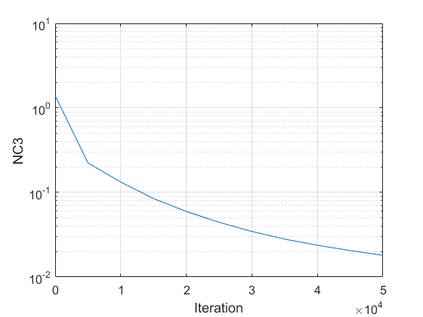
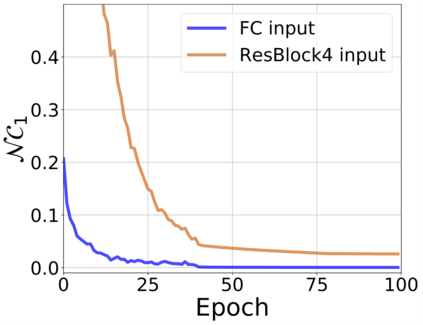
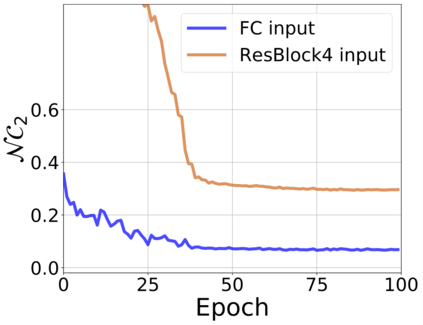
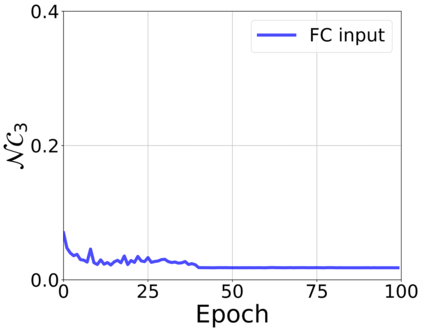
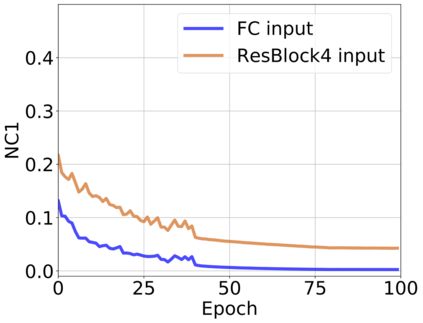
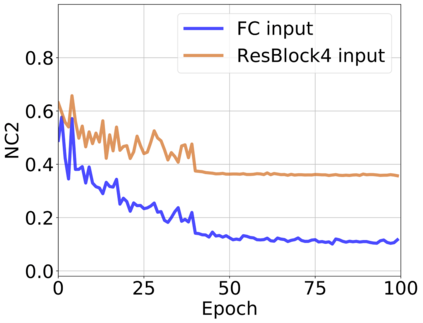
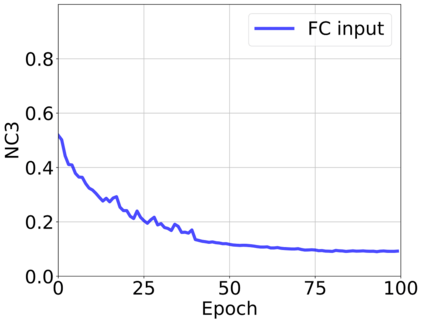
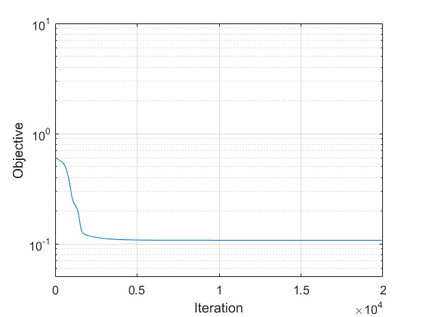
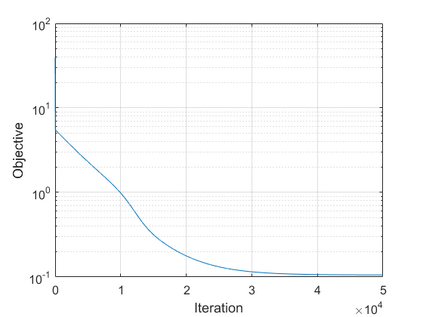
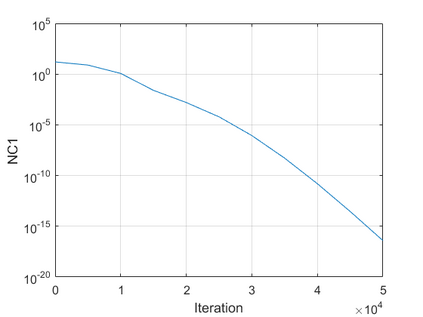
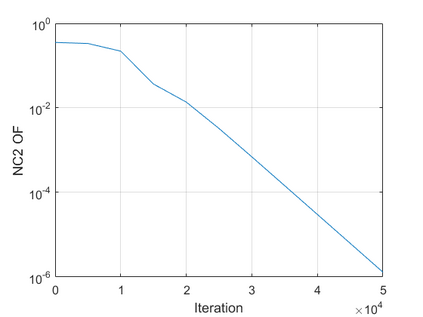
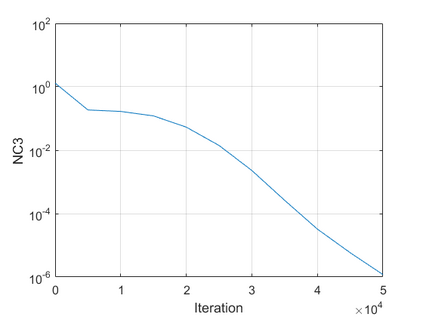
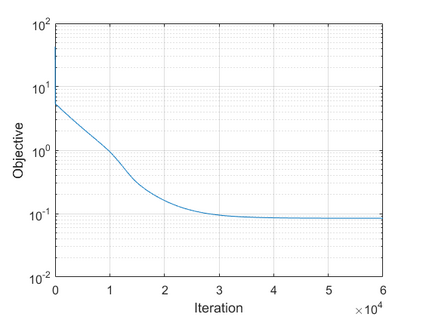
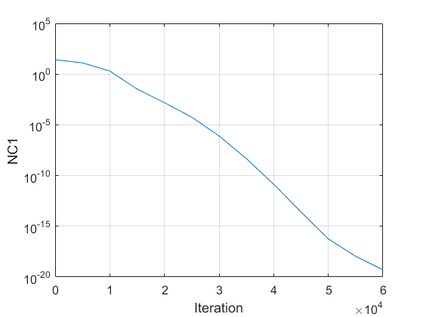
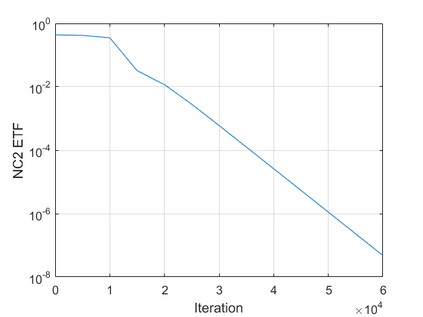
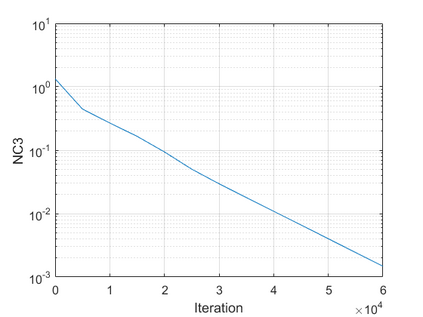
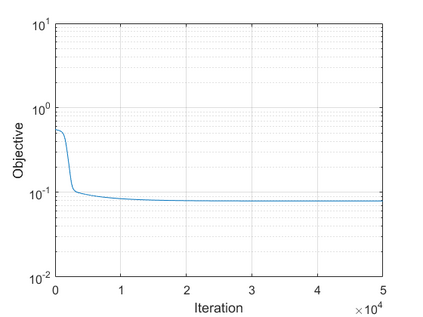
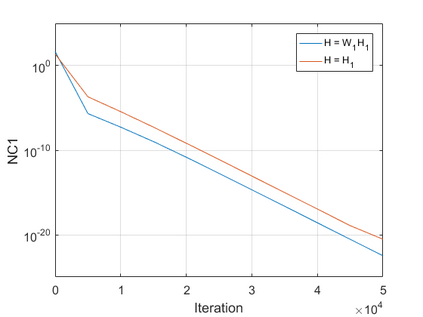
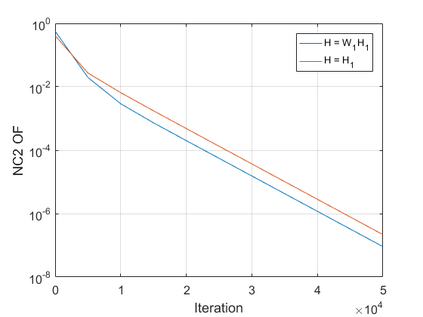
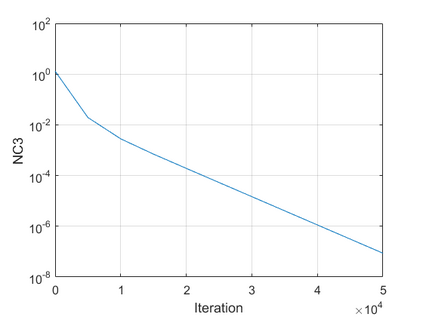
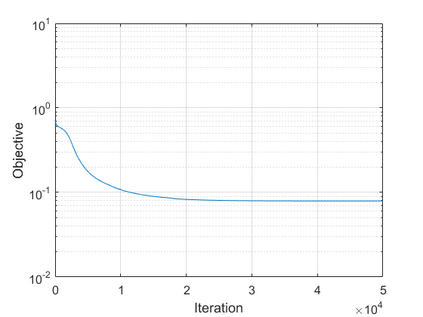
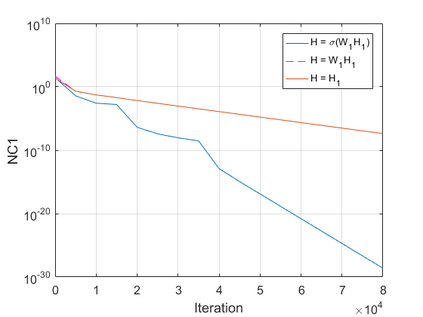
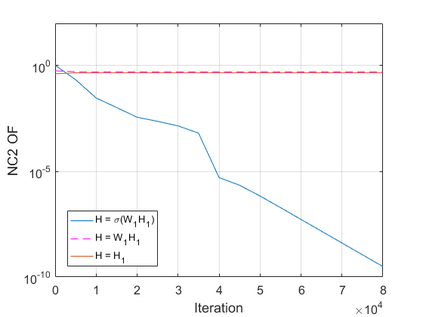
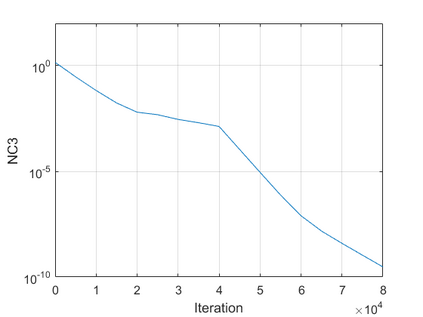
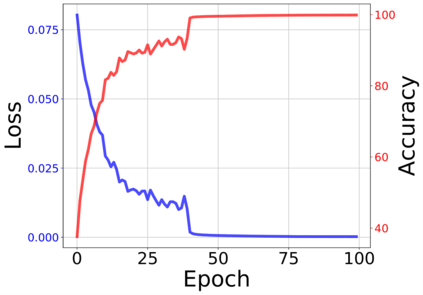
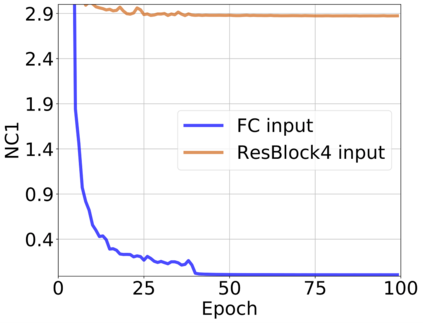
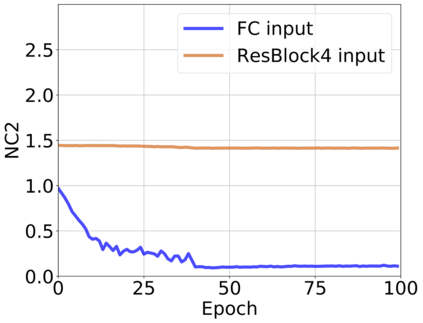
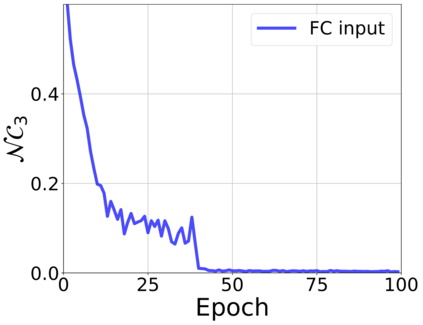
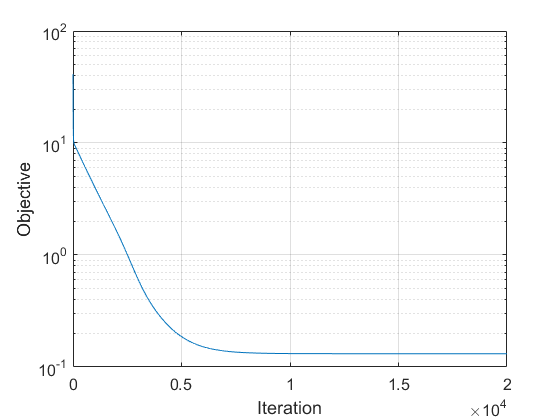
The modern strategy for training deep neural networks for classification tasks includes optimizing the network's weights even after the training error vanishes to further push the training loss toward zero. Recently, a phenomenon termed "neural collapse" (NC) has been empirically observed in this training procedure. Specifically, it has been shown that the learned features (the output of the penultimate layer) of within-class samples converge to their mean, and the means of different classes exhibit a certain tight frame structure, which is also aligned with the last layer's weights. Recent papers have shown that minimizers with this structure emerge when optimizing a simplified "unconstrained features model" (UFM) with a regularized cross-entropy loss. In this paper, we further analyze and extend the UFM. First, we study the UFM for the regularized MSE loss, and show that the minimizers' features can be more structured than in the cross-entropy case. This affects also the structure of the weights. Then, we extend the UFM by adding another layer of weights as well as ReLU nonlinearity to the model and generalize our previous results. Finally, we empirically demonstrate the usefulness of our nonlinear extended UFM in modeling the NC phenomenon that occurs with practical networks.