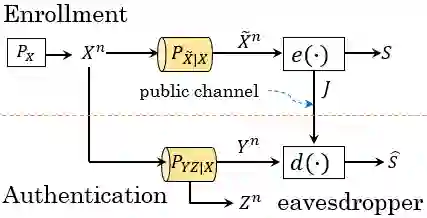
Secret-Key Agreement Using Physical Identifiers for Degraded and Less Noisy Authentication Channels

Secret-key agreement based on biometric or physical identifiers is a promising security protocol for authenticating users or devices with small chips and has been extensively studied recently. Kittichokechai and Caire (2015) investigated the optimal trade-off in a secret-key agreement model with physical identifiers, where the structure of the authentication channels is similar to the wiretap channels, from information-theoretic approaches. Later, the model was extended by G\"unl\"u et al.\ (2018) introducing noise in the enrollment phase and cost-constrained actions at the decoder. The results of these studies show that two auxiliary random variables are involved in the expressions of the optimal rate regions of secret-key, storage, and privacy-leakage rates. However, with these two auxiliary random variables, the complexity of computing the rate region may be prohibitively high. Due to this problem, we are interested in exploring classes of authentication channels that need only one auxiliary random variable in the capacity region expression for discrete source settings. The result shows for the class of degraded and less noisy authentication channels, a single auxiliary random variable is sufficient to express the capacity region of the model. As an example, we also derive the capacity region of secret-key, storage, and privacy-leakage rates for binary sources. Furthermore, the capacity region for scalar Gaussian sources is derived under Gaussian authentication channels.