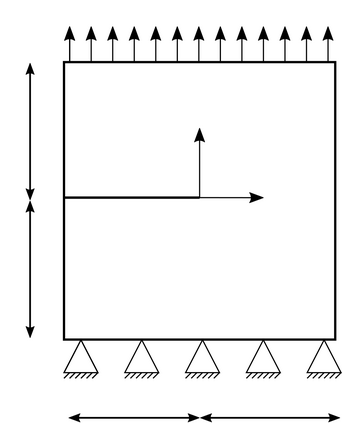
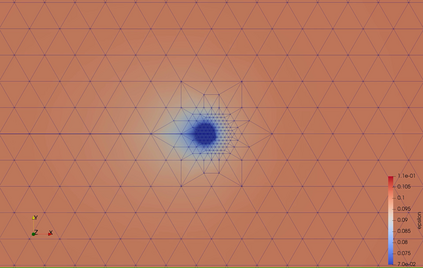
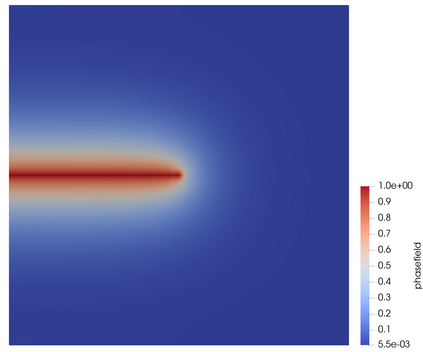
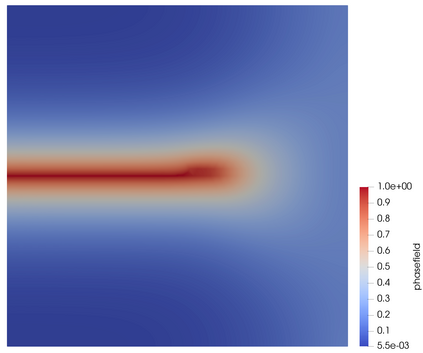
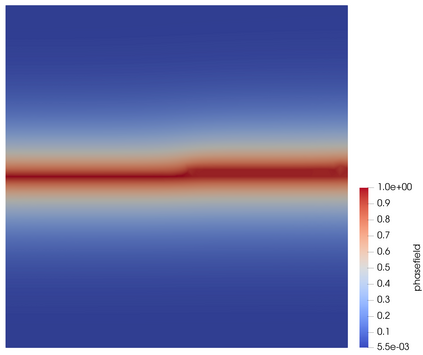
Phase-field models of fracture introduce smeared cracks of width commensurate with a regularisation length parameter $\epsilon$ and obeying a minimum energy principle. Mesh adaptivity naturally suggests itself as a means of supplying spatial resolution were needed while simultaneously keeping the computational size of the model as small as possible. Here, a variational-based spatial adaptivity is proposed for a phase-field model of fracture. The conventional phase-field model is generalised by allowing a spatial variation of the regularisation length $\epsilon$ in the energy functional. The optimal spatial variation of the regularisation length then follows by energy minimisation in the same manner as the displacement and phase fields. The extended phase-field model is utilised as a basis for an adaptive mesh refinement strategy, whereby the mesh size is required to resolve the optimal length parameter locally. The resulting solution procedure is implemented in the framework of the finite element library FEniCS. Selected numerical tests suggest that the spatially adaptive phase-field model exhibits the same convergence rate as the conventional phase-field model, albeit with a vastly superior constant, which results in considerable computational savings.
翻译:相片断裂形模型引入了与正常化参数($\ epsilon$)和符合最低能量原则相称的涂片宽度裂缝。 网状适应性自然表明自己是提供空间分辨率的一种手段, 同时需要将模型的计算大小尽可能小。 在此, 提出了一个基于不同空间的适切性模型, 用于分阶段断裂型模型。 常规的相位模型通过在能量功能中允许对正常化长度( $\ epsilon$)的空间差异进行空间差异来加以概括。 规范化长度的最佳空间差异随后以与位移和阶段字段相同的方式进行能源最小化。 扩展的战区模型被用作适应性网格精细化战略的基础, 从而需要网格大小来在当地解决最佳长度参数。 由此产生的解决方案程序在有限元素库 FENICS 的框架内实施。 某些数字测试表明, 空间适应性阶段模型显示与常规的相位模型相同的趋近率, 尽管常值非常高, 从而可以实现相当的计算节约。