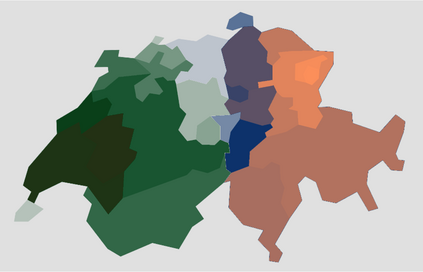
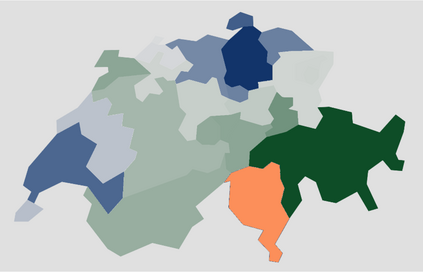
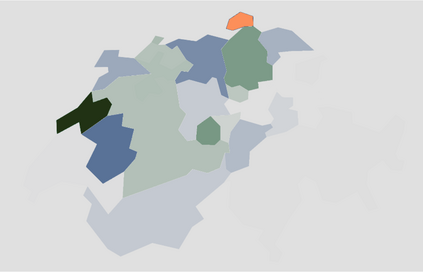
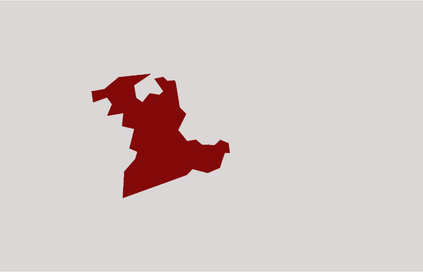
Adaptive spectral (AS) decompositions associated with a piecewise constant function $u$ yield small subspaces where the characteristic functions comprising $u$ are well approximated. When combined with Newton-like optimization methods for the solution of inverse medium problems, AS decompositions have proved remarkably efficient in providing at each nonlinear iteration a low-dimensional search space. Here, we derive $L^2$-error estimates for the AS decomposition of $u$, truncated after $K$ terms, when $u$ is piecewise constant and consists of $K$ characteristic functions over Lipschitz domains and a background. Our estimates apply both to the continuous and the discrete Galerkin finite element setting. Numerical examples illustrate the accuracy of the AS decomposition for media that either do, or do not, satisfy the assumptions of the theory.
翻译:与片段常量函数相关的适应性光谱分解(AS) $u美元产生小型子空间,其中由美元构成的特性功能非常接近于美元。当与类似牛顿的优化方法相结合解决反介质问题时,AS分解在为每个非线性迭代提供低维搜索空间方面证明非常有效。在这里,我们为AS的分解(美元)得出了价值为2美元/升的估计数,在美元条件之后,当美元是分解的常数,在利普西茨域域和背景上由1美元/美元构成。我们的估计适用于连续和离散的加勒金定点元素设置。数字示例显示了AS对符合理论假设或不符合理论假设的媒体的分解的准确性。