Symmetrized semi-discrete optimal transport

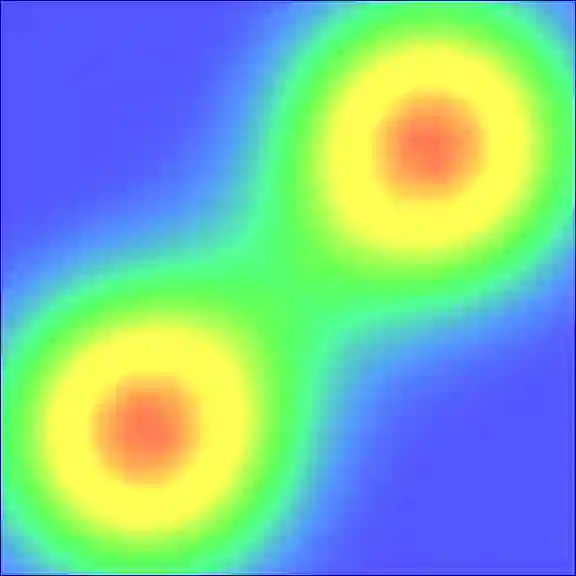
Interpolating between measures supported by polygonal or polyhedral domains is a problem that has been recently addressed by the semi-discrete optimal transport framework. Within this framework, one of the domains is discretized with a set of samples, while the other one remains continuous. In this paper we present a method to introduce some symmetry into the solution using coupled power diagrams. This symmetry is key to capturing the discontinuities of the transport map reflected in the geometry of the power cells. We design our method as a fixed-point algorithm alternating between computations of semi-discrete transport maps and recentering of the sites. The resulting objects are coupled power diagrams with identical geometry, allowing us to approximate displacement interpolation through linear interpolation of the meshes vertices. Through these coupled power diagrams, we have a natural way of jointly sampling measures.