Exact Matrix Factorization Updates for Nonlinear Programming

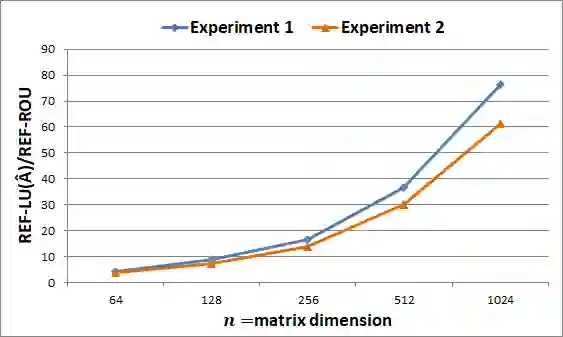
LU and Cholesky matrix factorization algorithms are core subroutines used to solve systems of linear equations (SLEs) encountered while solving an optimization problem. Standard factorization algorithms are highly efficient but remain susceptible to the accumulation of roundoff errors, which can lead solvers to return feasibility and optimality claims that are actually invalid. This paper introduces a novel approach for solving sequences of closely related SLEs encountered in nonlinear programming efficiently and without roundoff errors. Specifically, it introduces rank-one update algorithms for the roundoff-error-free (REF) factorization framework, a toolset built on integer-preserving arithmetic that has led to the development and implementation of fail-proof SLE solution subroutines for linear programming. The formal guarantees of the proposed algorithms are established through the derivation of theoretical insights. Their advantages are supported with computational experiments, which demonstrate upwards of 75x-improvements over exact factorization run-times on fully dense matrices with over one million entries. A significant advantage of the methodology is that the length of any coefficient calculated via the proposed algorithms is bounded polynomially in the size of the inputs without having to resort to greatest common divisor operations, which are required by and thereby hinder an efficient implementation of exact rational arithmetic approaches.