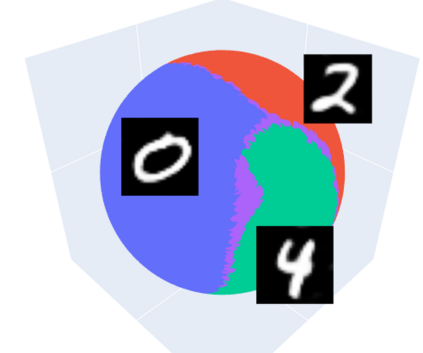
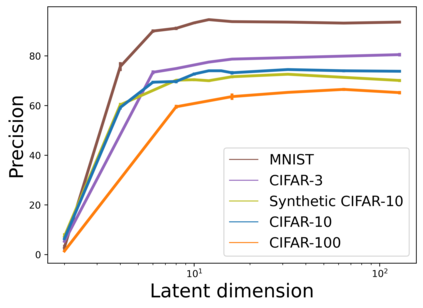
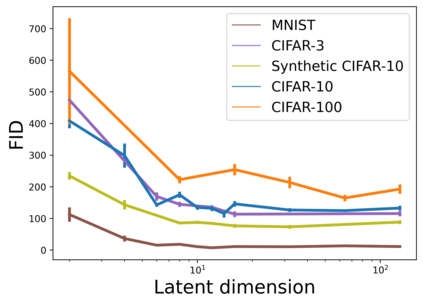
When learning disconnected distributions, Generative adversarial networks (GANs) are known to face model misspecification. Indeed, a continuous mapping from a unimodal latent distribution to a disconnected one is impossible, so GANs necessarily generate samples outside of the support of the target distribution. This raises a fundamental question: what is the latent space partition that minimizes the measure of these areas? Building on a recent result of geometric measure theory, we prove that an optimal GANs must structure its latent space as a 'simplicial cluster' - a Voronoi partition where cells are convex cones - when the dimension of the latent space is larger than the number of modes. In this configuration, each Voronoi cell maps to a distinct mode of the data. We derive both an upper and a lower bound on the optimal precision of GANs learning disconnected manifolds. Interestingly, these two bounds have the same order of decrease: $\sqrt{\log m}$, $m$ being the number of modes. Finally, we perform several experiments to exhibit the geometry of the latent space and experimentally show that GANs have a geometry with similar properties to the theoretical one.
翻译:当学习断开分布时, 已知生成对抗网络( GANs) 将面临模型错误的特性。 事实上, 从单模式潜在分布到断开的连续映射是不可能的, 所以 GANs 必然会在目标分布支持之外生成样本。 这就提出了一个根本性的问题: 隐藏空间分区是什么样的, 能将这些地区的测量量最小化? 基于最近几何测量理论的结果, 我们证明最佳的 GANs 必须将其潜在空间构造成一个“ 隐性聚集 ”, 也就是一个Voronoi 分区, 它的单元格是锥形—— 当潜伏空间的尺寸大于模式数时。 在这个配置中, 每个Voronoi 单元格都绘制到数据的不同模式。 我们根据GANs 学习的优化精度来得出一个上下圈和下圈。 有趣的是, 这两个边框有相同的递减顺序 : $\\\ qrt\ m} $, $m$m美元是模式的数量 。 最后, 我们进行了几次实验以展示隐性空间的几何测量, 并且实验显示GAN具有相似的理论性。