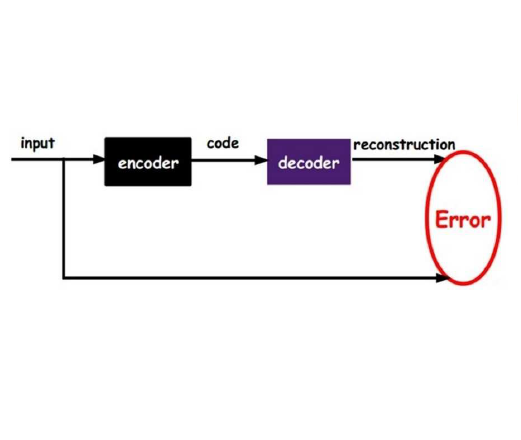
Recent progress in Generative Artificial Intelligence (AI) relies on efficient data representations, often featuring encoder-decoder architectures. We formalize the mathematical problem of finding the optimal encoder-decoder pair and characterize its solution, which we name the "benign autoencoder" (BAE). We prove that BAE projects data onto a manifold whose dimension is the optimal compressibility dimension of the generative problem. We highlight surprising connections between BAE and several recent developments in AI, such as conditional GANs, context encoders, stable diffusion, stacked autoencoders, and the learning capabilities of generative models. As an illustration, we show how BAE can find optimal, low-dimensional latent representations that improve the performance of a discriminator under a distribution shift. By compressing "malignant" data dimensions, BAE leads to smoother and more stable gradients.
翻译:暂无翻译