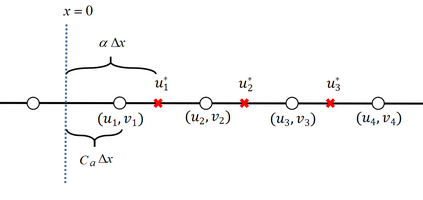
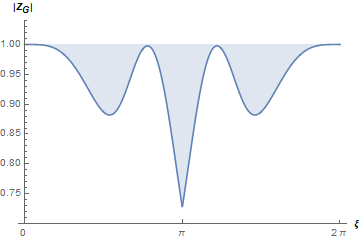
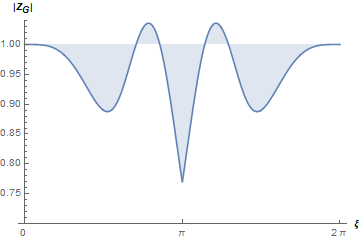
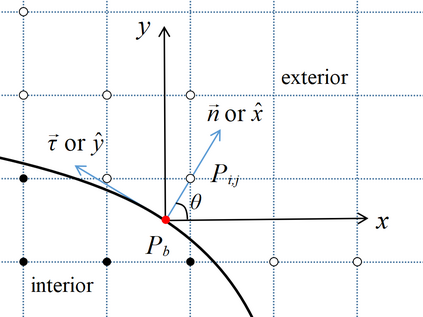
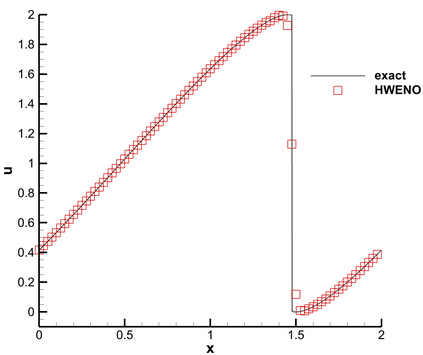
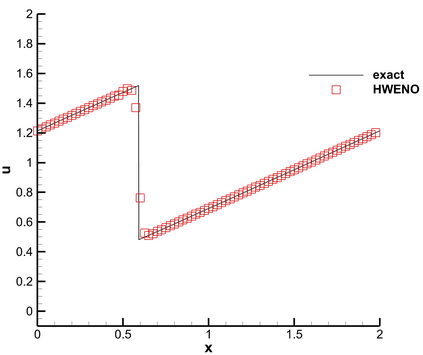
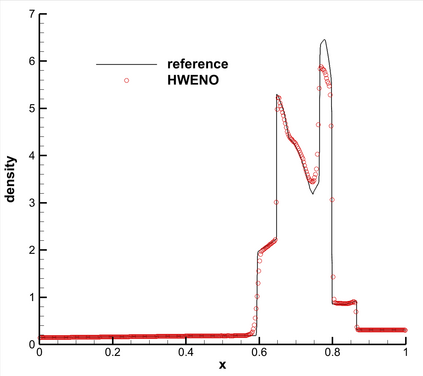
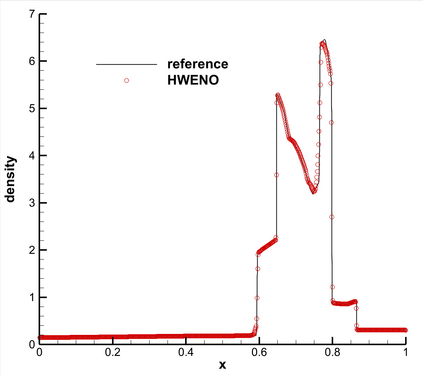
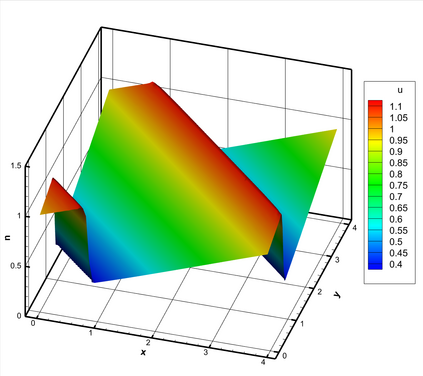
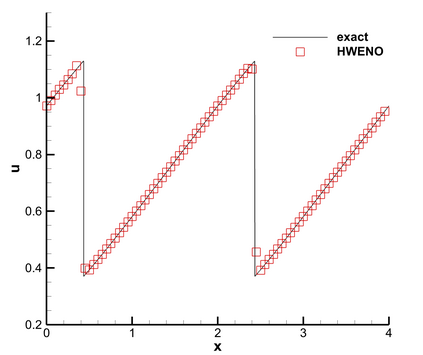
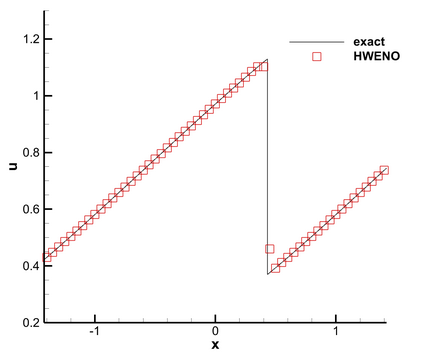
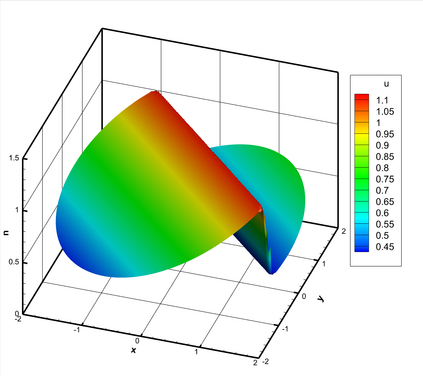
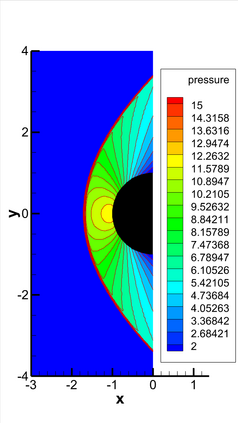
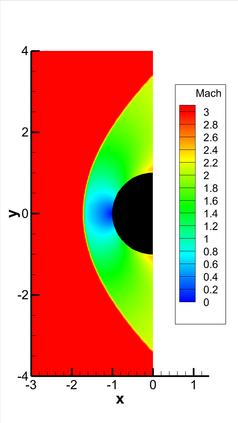
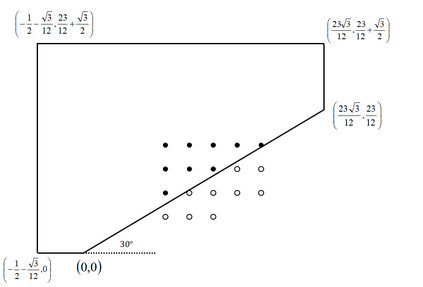
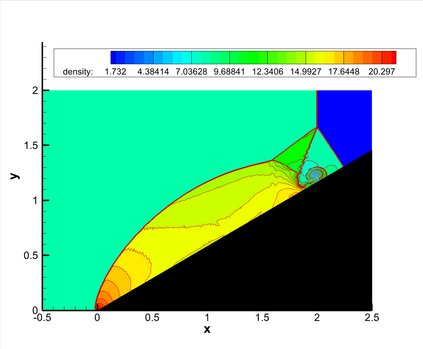
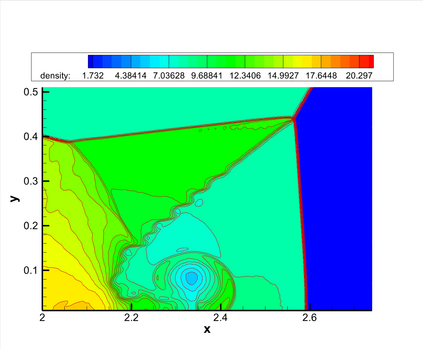
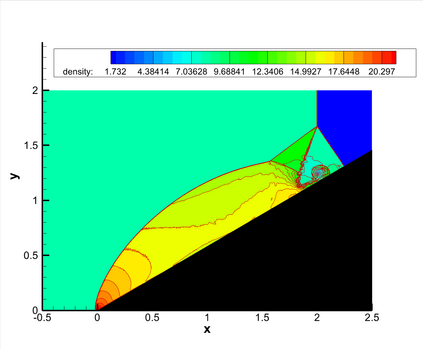
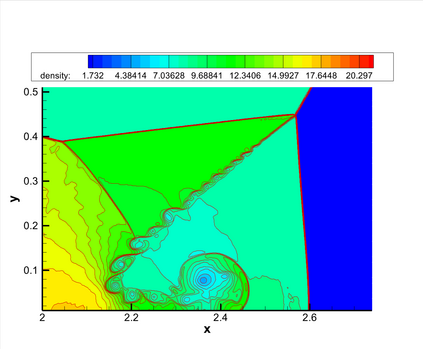
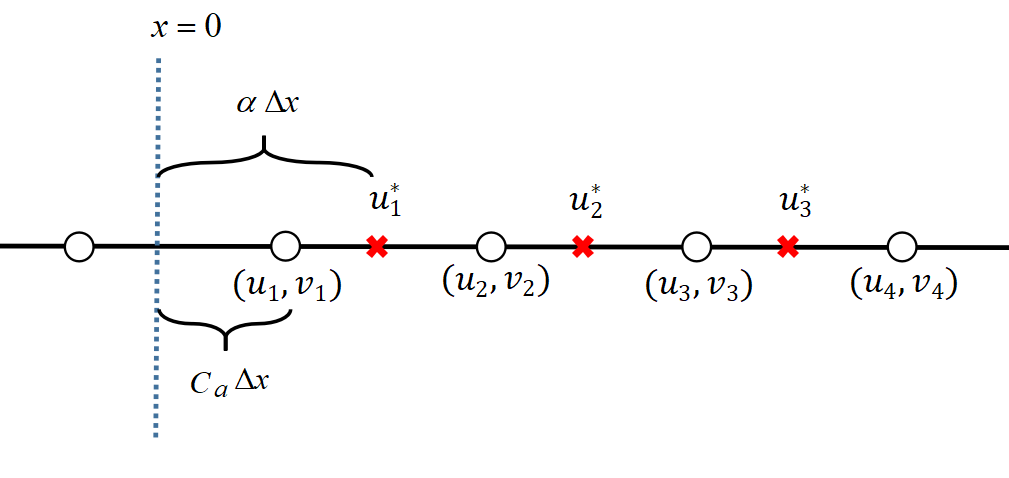
This paper presents a novel inverse Lax-Wendroff (ILW) boundary treatment for finite difference Hermite weighted essentially non-oscillatory (HWENO) schemes to solve hyperbolic conservation laws on arbitrary geometries. The complex geometric domain is divided by a uniform Cartesian grid, resulting in challenge in boundary treatment. The proposed ILW boundary treatment could provide high order approximations of both solution values and spatial derivatives at ghost points outside the computational domain. Distinct from existing ILW approaches, our boundary treatment constructs the extrapolation via optimized through a least squares formulation, coupled with the spatial derivatives at the boundary obtained via the ILW procedure. Theoretical analysis indicates that compared with other ILW methods, our proposed one would require fewer terms by using the relatively complicated ILW procedure and thus improve computational efficiency while preserving accuracy and stability. The effectiveness and robustness of the method are validated through numerical experiments.
翻译:暂无翻译