Recovery of transversely-isotropic elastic material parameters in induction motor rotors

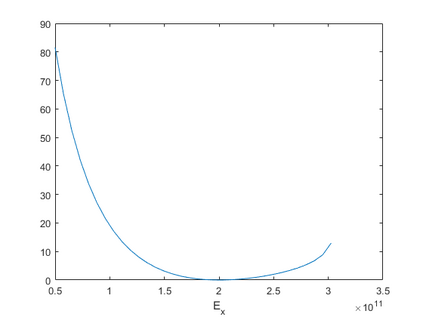
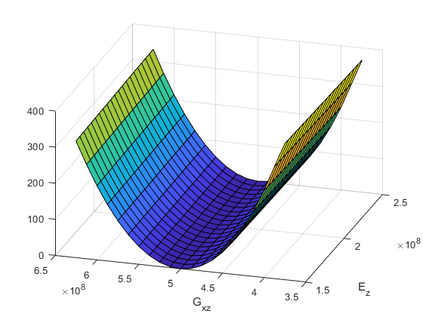
We propose numerical algorithms for recovering parameters in eigenvalue problems for linear elasticity of transversely isotropic materials. Specifically, the algorithms are used to recover the elastic constants of a rotor core. Numerical tests show that in the noiseless setup, two pairs of bending modes are sufficient for recovering one to four parameters accurately. To recover all five parameters that govern the elastic properties of electric engines accurately, we require three pairs of bending modes and one torsional mode. Moreover, we study the stability of the inversion method against multiplicative noise; for tests in which the data contained multiplicative noise of at most $1\%$, we find that all parameters can be recovered with an error less than $10\%$.