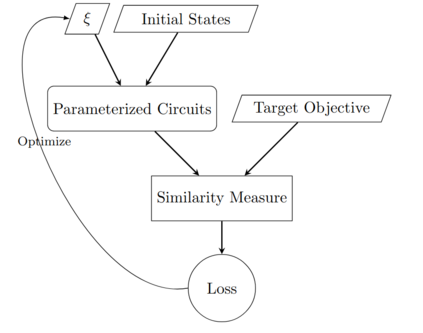
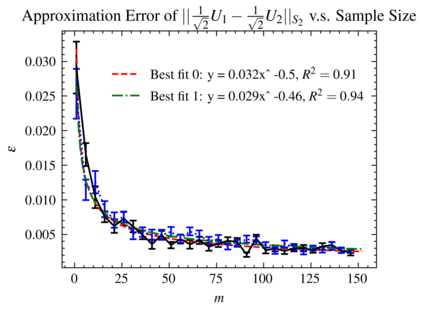
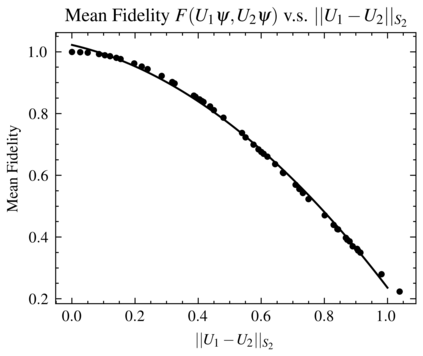
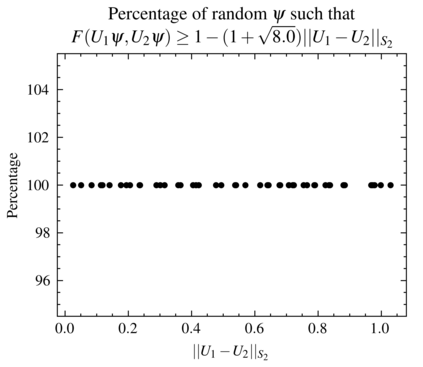
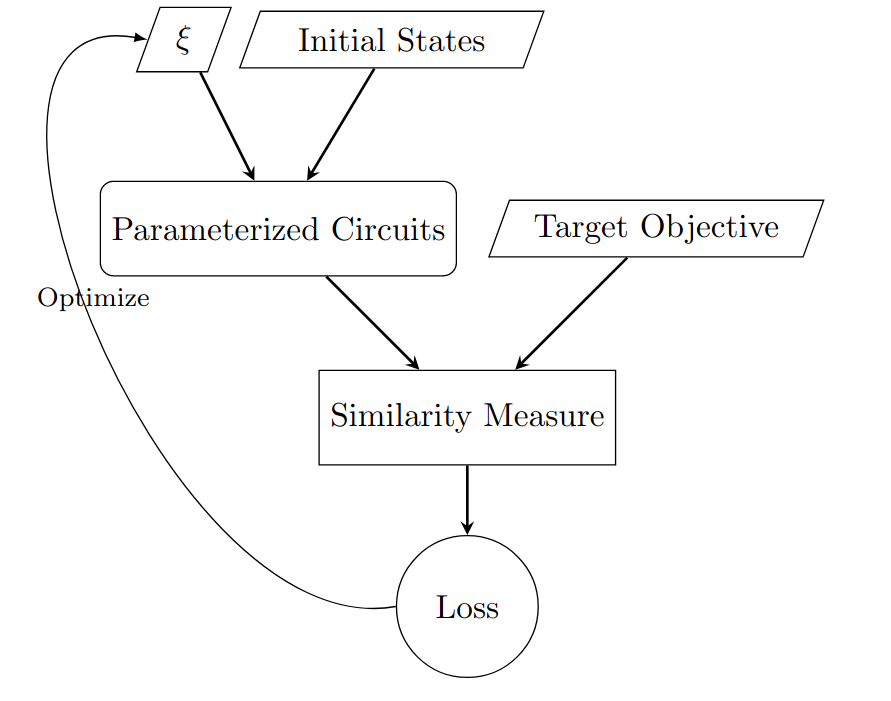
Efficient measures to determine similarity of quantum states, such as the fidelity metric, have been widely studied. In this paper, we address the problem of defining a similarity measure for quantum operations that can be \textit{efficiently estimated}. Given two quantum operations, $U_1$ and $U_2$, represented in their circuit forms, we first develop a quantum sampling circuit to estimate the normalized Schatten 2-norm of their difference ($\| U_1-U_2 \|_{S_2}$) with precision $\epsilon$, using only one clean qubit and one classical random variable. We prove a Poly$(\frac{1}{\epsilon})$ upper bound on the sample complexity, which is independent of the size of the quantum system. We then show that such a similarity metric is directly related to a functional definition of similarity of unitary operations using the conventional fidelity metric of quantum states ($F$): If $\| U_1-U_2 \|_{S_2}$ is sufficiently small (e.g. $ \leq \frac{\epsilon}{1+\sqrt{2(1/\delta - 1)}}$) then the fidelity of states obtained by processing the same randomly and uniformly picked pure state, $|\psi \rangle$, is as high as needed ($F({U}_1 |\psi \rangle, {U}_2 |\psi \rangle)\geq 1-\epsilon$) with probability exceeding $1-\delta$. We provide example applications of this efficient similarity metric estimation framework to quantum circuit learning tasks, such as finding the square root of a given unitary operation.
翻译:确定量子状态相似性的有效度量措施, 如忠诚度度度等, 已经进行了广泛的研究。 在本文中, 我们只用一个干净的qubit 和一个古典随机变量来定义量子操作的类似度量量度。 鉴于其电路形式的两种量量值操作, 即$_ 1美元和$2美元, 我们首先开发一个量子采样电路, 来估计其差值的归正沙坦 2- 温度值( U_ 1 - U_ 2 美元) 和精确 $( epsility qbit) 和一个古典随机变量。 我们证明, 在样本复杂性上, 美元(\\ lec{ 1\\\ ~ eepsil} 美元, 与量子系统大小无关。 我们然后显示, 类似度的量子量值测量值直接与统一操作的功能定义相近似性, 使用通常的量度度度度度度度度度度度度度度度量值测量值( $_ 1- U_ __ =xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx