Asymptotics of multivariate sequences IV: generating functions with poles on a hyperplane arrangement

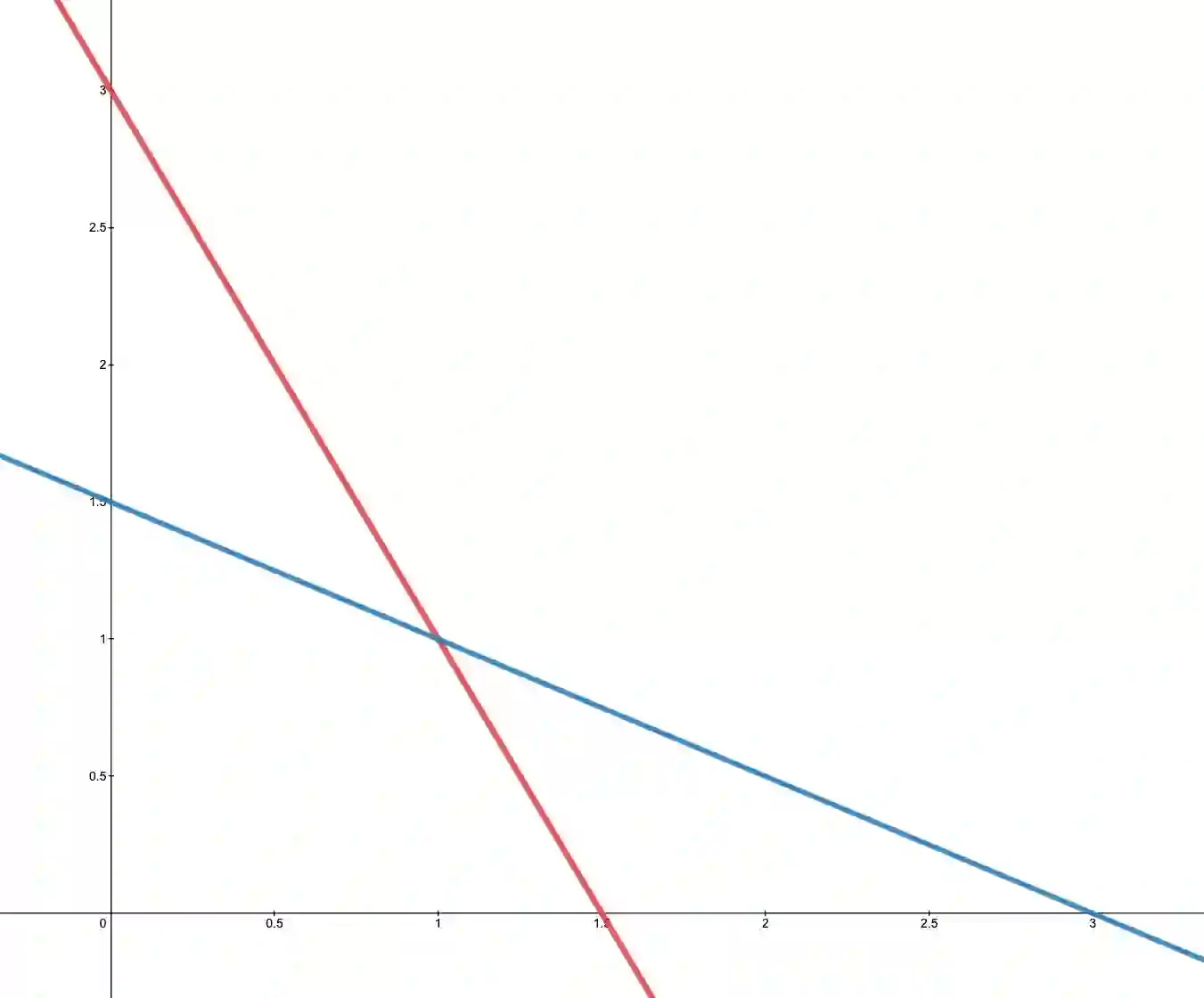
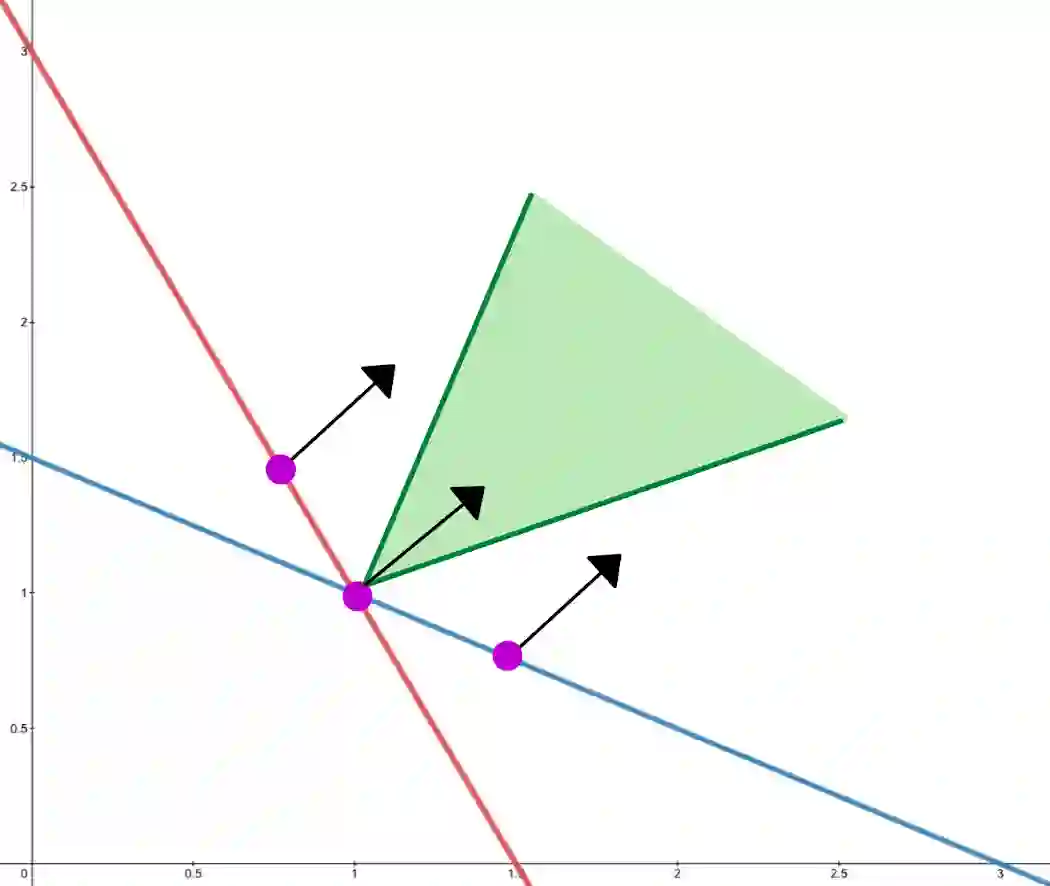
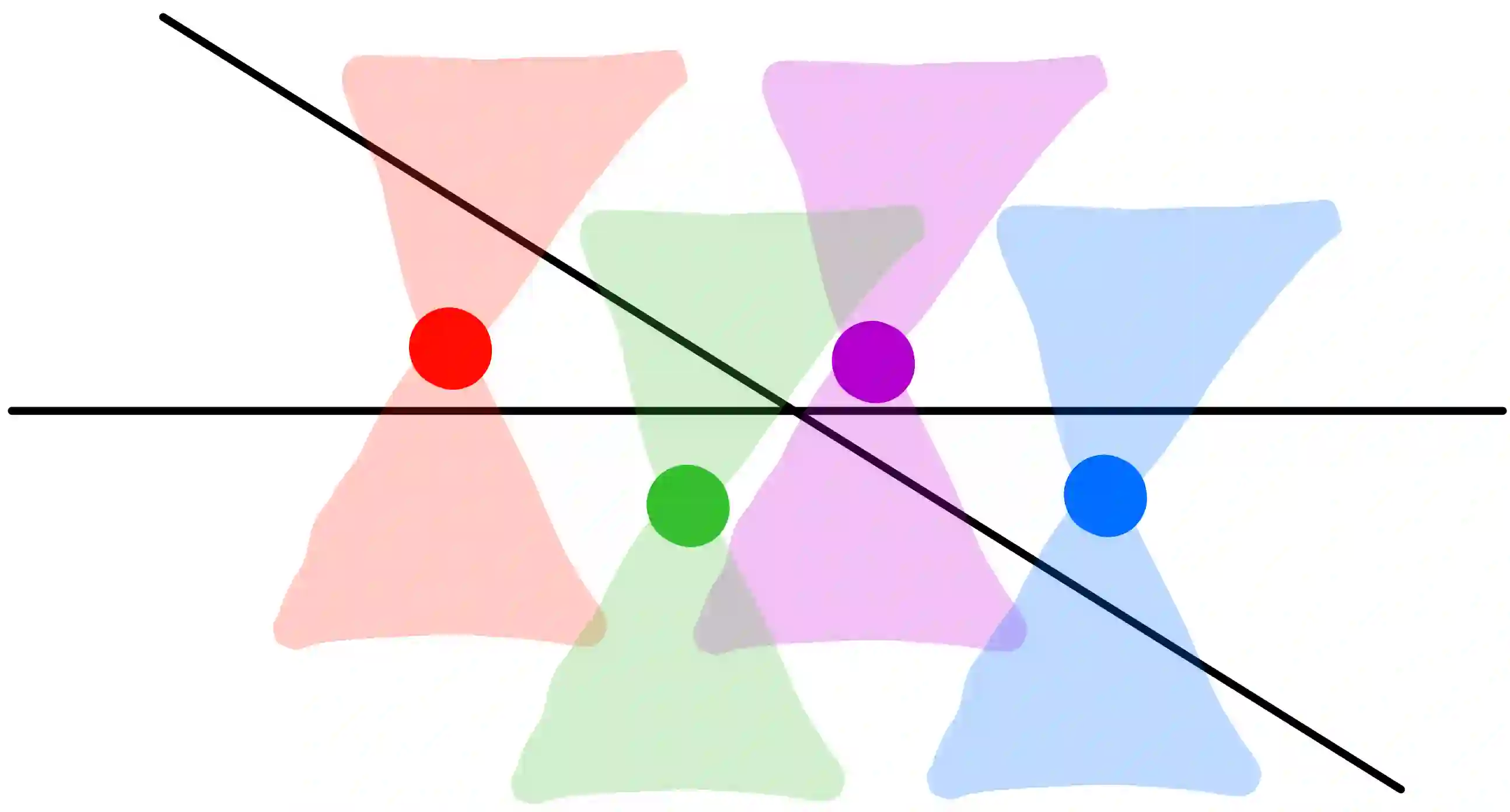
Let F be the quotient of an analytic function with a product of linear functions. Working in the framework of analytic combinatorics in several variables, we compute asymptotic formulae for the Taylor coefficients of F using multivariate residues and saddle-point approximations. Because the singular set of F is the union of hyperplanes, we are able to make explicit the topological decompositions which arise in the multivariate singularity analysis. In addition to effective and explicit asymptotic results, we provide the first results on transitions between different asymptotic regimes, and provide the first software package to verify and compute asymptotics in non-smooth cases of analytic combinatorics in several variables. It is also our hope that this paper will serve as an entry to the more advanced corners of analytic combinatorics in several variables for combinatorialists.